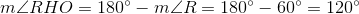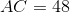Rhombuses
Help Questions
PSAT Math › Rhombuses
In Rhombus 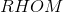








Explanation
The figure referenced is below.

Consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
A similar argument proves that 
Since all three angles of 

In Rhombus 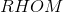








Explanation
The figure referenced is below.

Consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
A similar argument proves that 
Since all three angles of 

If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.
24
20
16
12
8
Explanation
The area of a rhombus is found by
A = 1/2(_d_1)(_d_2)
where _d_1 and _d_2 are the lengths of the diagonals. Substituting for the given values yields
24 = 1/2(_d_1)(6)
24 = 3(_d_1)
8 = _d_1
Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 32 + 42 = 52, each side length is 5, so the perimeter is 5(4) = 20.
If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.
24
20
16
12
8
Explanation
The area of a rhombus is found by
A = 1/2(_d_1)(_d_2)
where _d_1 and _d_2 are the lengths of the diagonals. Substituting for the given values yields
24 = 1/2(_d_1)(6)
24 = 3(_d_1)
8 = _d_1
Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 32 + 42 = 52, each side length is 5, so the perimeter is 5(4) = 20.

Note: Figure NOT drawn to scale.
Calculate the perimeter of Quadrilateral 
Insufficient information is given to answer the question.
Explanation



We focus on 
By the Pythagorean Theorem,
26 is the common length of the four sides of Quadrilateral 


Note: Figure NOT drawn to scale.
Calculate the perimeter of Quadrilateral 
Insufficient information is given to answer the question.
Explanation



We focus on 
By the Pythagorean Theorem,
26 is the common length of the four sides of Quadrilateral 

A rhombus has a side length of 5. Which of the following is NOT a possible value for its area?
25
24
10
15
30
Explanation
The area of a rhombus will vary as the angles made by its sides change. The "flatter" the rhombus is (with two very small angles and two very large angles, say 2, 178, 2, and 178 degrees), the smaller the area is. There is, of course, a lower bound of zero for the area, but the area can get arbitrarily small. This implies that the correct answer would be the largest choice. In fact, the largest area of a rhombus occurs when all four angles are equal, i.e. when the rhombus is a square. The area of a square of side length 5 is 25, so any value bigger than 25 is impossible to acheive.
A rhombus has a side length of 5. Which of the following is NOT a possible value for its area?
25
24
10
15
30
Explanation
The area of a rhombus will vary as the angles made by its sides change. The "flatter" the rhombus is (with two very small angles and two very large angles, say 2, 178, 2, and 178 degrees), the smaller the area is. There is, of course, a lower bound of zero for the area, but the area can get arbitrarily small. This implies that the correct answer would be the largest choice. In fact, the largest area of a rhombus occurs when all four angles are equal, i.e. when the rhombus is a square. The area of a square of side length 5 is 25, so any value bigger than 25 is impossible to acheive.
In Rhombus 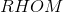








Explanation
The figure referenced is below.

The sides of a rhombus are congruent by definition, so 



Also, consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
Similarly,
This makes 
The correct response is that 
In Rhombus 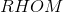








Explanation
The figure referenced is below.

The sides of a rhombus are congruent by definition, so 



Also, consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so
A diagonal of a rhombus bisects its angles, so
Similarly,
This makes 
The correct response is that