Quadrilaterals - PSAT Math
Card 1 of 399
ABCD is a parallelogram. BD = 5. The angles of triangle ABD are all equal. What is the perimeter of the parallelogram?
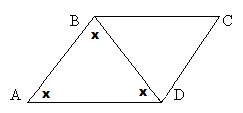
ABCD is a parallelogram. BD = 5. The angles of triangle ABD are all equal. What is the perimeter of the parallelogram?

Tap to reveal answer
If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.
We now have two equilateral triangles, so all sides of the triangles will be equal.
All sides therefore equal 5.
5+5+5+5 = 20
If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.
We now have two equilateral triangles, so all sides of the triangles will be equal.
All sides therefore equal 5.
5+5+5+5 = 20
← Didn't Know|Knew It →

Rectangle ABCD is shown in the figure above. Points A and B lie on the graph of y = 64 – _x_2 , and points C and D lie on the graph of y = _x_2 – 36. Segments AD and BC are both parallel to the y-axis. The x-coordinates of points A and B are equal to –k and k, respectively. If the value of k changes from 2 to 4, by how much will the area of rectangle ABCD increase?
Rectangle ABCD is shown in the figure above. Points A and B lie on the graph of y = 64 – _x_2 , and points C and D lie on the graph of y = _x_2 – 36. Segments AD and BC are both parallel to the y-axis. The x-coordinates of points A and B are equal to –k and k, respectively. If the value of k changes from 2 to 4, by how much will the area of rectangle ABCD increase?
Tap to reveal answer
← Didn't Know|Knew It →
A contractor is going to re-tile a rectangular section of the kitchen floor. If the floor is 6ft x 3ft, and he is going to use square tiles with a side of 9in. How many tiles will be needed?
A contractor is going to re-tile a rectangular section of the kitchen floor. If the floor is 6ft x 3ft, and he is going to use square tiles with a side of 9in. How many tiles will be needed?
Tap to reveal answer
We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)
We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)
← Didn't Know|Knew It →
If the area Rectangle A is  larger than Rectangle B and the sides of Rectangle A are
larger than Rectangle B and the sides of Rectangle A are  and
and  , what is the area of Rectangle B?
, what is the area of Rectangle B?
If the area Rectangle A is 


Tap to reveal answer
← Didn't Know|Knew It →
The front façade of a building is 100 feet tall and 40 feet wide. There are eight floors in the building, and each floor has four glass windows that are 8 feet wide and 6 feet tall along the front façade. What is the total area of the glass in the façade?
The front façade of a building is 100 feet tall and 40 feet wide. There are eight floors in the building, and each floor has four glass windows that are 8 feet wide and 6 feet tall along the front façade. What is the total area of the glass in the façade?
Tap to reveal answer
Glass Area per Window = 8 ft x 6 ft = 48 ft2
Total Number of Windows = Windows per Floor * Number of Floors = 4 * 8 = 32 windows
Total Area of Glass = Area per Window * Total Number of Windows = 48 * 32 = 1536 ft2
Glass Area per Window = 8 ft x 6 ft = 48 ft2
Total Number of Windows = Windows per Floor * Number of Floors = 4 * 8 = 32 windows
Total Area of Glass = Area per Window * Total Number of Windows = 48 * 32 = 1536 ft2
← Didn't Know|Knew It →
The rectangular bathroom floor in Michael’s house is ten feet by twelve feet. He wants to purchase square tiles that are four inches long and four inches wide to cover the bathroom floor. If each square tile costs $2.50, how much money will Michael need to spend in order to purchase enough tiles to cover his entire bathroom floor?
The rectangular bathroom floor in Michael’s house is ten feet by twelve feet. He wants to purchase square tiles that are four inches long and four inches wide to cover the bathroom floor. If each square tile costs $2.50, how much money will Michael need to spend in order to purchase enough tiles to cover his entire bathroom floor?
Tap to reveal answer
The dimensions for the bathroom are given in feet, but the dimensions of the tiles are given in inches; therefore, we need to convert the dimensions of the bathroom from feet to inches, because we can’t compare measurements easily unless we are using the same type of units.
Because there are twelve inches in a foot, we need to multiply the number of feet by twelve to convert from feet to inches.
10 feet = 10 x 12 inches = 120 inches
12 feet = 12 x 12 inches = 144 inches
This means that the bathroom floor is 120 inches by 144 inches. The area of Michael’s bathroom is therefore 120 x 144 in2 = 17280 in2.
Now, we need to find the area of the tiles in square inches and calculate how many tiles it would take to cover 17280 in2.
Each tile is 4 in by 4 in, so the area of each tile is 4 x 4 in2, or 16 in2.
If there are 17280 in2 to be covered, and each tile is 16 in2, then the number of tiles we need is 17280 ÷ 16, which is 1080 tiles.
The question ultimately asks us for the cost of all these tiles; therefore, we need to multiply 1080 by 2.50, which is the price of each tile.
The total cost = 1080 x 2.50 dollars = 2700 dollars.
The answer is $2700.
The dimensions for the bathroom are given in feet, but the dimensions of the tiles are given in inches; therefore, we need to convert the dimensions of the bathroom from feet to inches, because we can’t compare measurements easily unless we are using the same type of units.
Because there are twelve inches in a foot, we need to multiply the number of feet by twelve to convert from feet to inches.
10 feet = 10 x 12 inches = 120 inches
12 feet = 12 x 12 inches = 144 inches
This means that the bathroom floor is 120 inches by 144 inches. The area of Michael’s bathroom is therefore 120 x 144 in2 = 17280 in2.
Now, we need to find the area of the tiles in square inches and calculate how many tiles it would take to cover 17280 in2.
Each tile is 4 in by 4 in, so the area of each tile is 4 x 4 in2, or 16 in2.
If there are 17280 in2 to be covered, and each tile is 16 in2, then the number of tiles we need is 17280 ÷ 16, which is 1080 tiles.
The question ultimately asks us for the cost of all these tiles; therefore, we need to multiply 1080 by 2.50, which is the price of each tile.
The total cost = 1080 x 2.50 dollars = 2700 dollars.
The answer is $2700.
← Didn't Know|Knew It →
Ron has a fixed length of wire that he uses to make a lot. On Monday, he uses the wire to make a rectangular lot. On Tuesday, he uses the same length of wire to form a square-shaped lot. Ron notices that the square lot has slightly more area, and he determines that the difference between the areas of the two lots is sixteen square units. What is the positive difference, in units, between the length and the width of the lot on Monday?
Ron has a fixed length of wire that he uses to make a lot. On Monday, he uses the wire to make a rectangular lot. On Tuesday, he uses the same length of wire to form a square-shaped lot. Ron notices that the square lot has slightly more area, and he determines that the difference between the areas of the two lots is sixteen square units. What is the positive difference, in units, between the length and the width of the lot on Monday?
Tap to reveal answer
Let’s say that the rectangular lot on Monday has a length of l and a width of w. The area of a rectangular is the product of the length and the width, so we can write the area of the lot on Monday as lw.
Next, we need to find an expression for the area of the lot on Tuesday. We are told that the lot is in the shape of a square and that it uses the same length of wire. If the length of the wire used is the same on both days, then the perimeter will have to remain the same. In other words, the perimeter of the square will equal the perimeter of the rectangle. The perimeter of a rectangle is given by 2_l_ + 2_w_.
We also know that if s is the length of a side of a square, then the perimeter is 4_s_, because each side of the square is congruent. Let’s write an equation that sets the perimeter of the rectangle and the square equal.
2_l_ + 2_w_ = 4_s_
If we divide both sides by 4 and then simplify the expression, then we can write the length of the square as follows:


Let’s say that the rectangular lot on Monday has a length of l and a width of w. The area of a rectangular is the product of the length and the width, so we can write the area of the lot on Monday as lw.
Next, we need to find an expression for the area of the lot on Tuesday. We are told that the lot is in the shape of a square and that it uses the same length of wire. If the length of the wire used is the same on both days, then the perimeter will have to remain the same. In other words, the perimeter of the square will equal the perimeter of the rectangle. The perimeter of a rectangle is given by 2_l_ + 2_w_.
We also know that if s is the length of a side of a square, then the perimeter is 4_s_, because each side of the square is congruent. Let’s write an equation that sets the perimeter of the rectangle and the square equal.
2_l_ + 2_w_ = 4_s_
If we divide both sides by 4 and then simplify the expression, then we can write the length of the square as follows:
← Didn't Know|Knew It →
A rectangle has a width of 2_x_. If the length is five more than 150% of the width, what is the area of the rectangle?
A rectangle has a width of 2_x_. If the length is five more than 150% of the width, what is the area of the rectangle?
Tap to reveal answer
Given that w = 2_x_ and l = 1.5_w_ + 5, a substitution will show that l = 1.5(2_x_) + 5 = 3_x_ + 5.
A = lw = (3_x_ + 5)(2_x_) = 6_x_2 + 10_x_
Given that w = 2_x_ and l = 1.5_w_ + 5, a substitution will show that l = 1.5(2_x_) + 5 = 3_x_ + 5.
A = lw = (3_x_ + 5)(2_x_) = 6_x_2 + 10_x_
← Didn't Know|Knew It →
Two circles of a radius of  each sit inside a square with a side length of
each sit inside a square with a side length of  . If the circles do not overlap, what is the area outside of the circles, but within the square?
. If the circles do not overlap, what is the area outside of the circles, but within the square?
Two circles of a radius of 

Tap to reveal answer
The area of a square = $side^{2}$
The area of a circle is pi $r^{2}$
Area = Area of Square - 2(Area of Circle) =


The area of a square = $side^{2}$
The area of a circle is pi $r^{2}$
Area = Area of Square - 2(Area of Circle) =
← Didn't Know|Knew It →
George wants to paint the walls in his room blue. The ceilings are 10 ft tall and a carpet 12 ft by 15 ft covers the floor. One gallon of paint covers 400 ft^{2} and costs $40. One quart of paint covers 100 ft^{2} and costs $15. How much money will he spend on the blue paint?
George wants to paint the walls in his room blue. The ceilings are 10 ft tall and a carpet 12 ft by 15 ft covers the floor. One gallon of paint covers 400 ft^{2} and costs $40. One quart of paint covers 100 ft^{2} and costs $15. How much money will he spend on the blue paint?
Tap to reveal answer
The area of the walls is given by 
One gallon of paint covers 400 ft^{2} and the remaining 140 ft^{2} would be covered by two quarts.
So one gallon and two quarts of paint would cost 
The area of the walls is given by
One gallon of paint covers 400 ft^{2} and the remaining 140 ft^{2} would be covered by two quarts.
So one gallon and two quarts of paint would cost
← Didn't Know|Knew It →
Daisy gets new carpet for her rectangluar room. Her floor is 21 ft times 24 ft. The carpet sells for $5 per square yard. How much did she spend on her carpet?
Daisy gets new carpet for her rectangluar room. Her floor is 21 ft times 24 ft. The carpet sells for $5 per square yard. How much did she spend on her carpet?
Tap to reveal answer
Since 3 ft=1 yd the room measurements are 7 yards by 8 yards. The area of the floor is thus 56 square yards. It would cost 5cdot 56=$280.
Since 3 ft=1 yd the room measurements are 7 yards by 8 yards. The area of the floor is thus 56 square yards. It would cost 5cdot 56=$280.
← Didn't Know|Knew It →
The length of a rectangular rug is five more than twice its width. The perimeter of the rug is 40 ft. What is the area of the rug?
The length of a rectangular rug is five more than twice its width. The perimeter of the rug is 40 ft. What is the area of the rug?
Tap to reveal answer
For a rectangle, P=2w+2l and A=lw where w is the width and l is the length.
Let x=width and 2x+5=length.
So the equation to solve becomes 40=2x+2(2x+5) or 40=6x+10.
Thus x=5 ft and 2x+5=15 ft, so the area is 75 $ft^{2}$.
For a rectangle, P=2w+2l and A=lw where w is the width and l is the length.
Let x=width and 2x+5=length.
So the equation to solve becomes 40=2x+2(2x+5) or 40=6x+10.
Thus x=5 ft and 2x+5=15 ft, so the area is 75 $ft^{2}$.
← Didn't Know|Knew It →

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in orange) eight feet wide throughout. What is the area of that dirt path?

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in orange) eight feet wide throughout. What is the area of that dirt path?
Tap to reveal answer
The dirt path can be seen as the region between two rectangles. The outer rectangle has length and width 100 feet and 60 feet, respectively, so its area is
 square feet.
square feet.
The inner rectangle has length and width  feet and
feet and  feet, respectively, so its area is
feet, respectively, so its area is
 square feet.
square feet.
The area of the path is the difference of the two:
 square feet.
square feet.
The dirt path can be seen as the region between two rectangles. The outer rectangle has length and width 100 feet and 60 feet, respectively, so its area is

The inner rectangle has length and width 


The area of the path is the difference of the two:

← Didn't Know|Knew It →

Note: Figure NOT drawn to scale

What percent of Rectangle  is pink?
is pink?

Note: Figure NOT drawn to scale
What percent of Rectangle 
Tap to reveal answer
The pink region is Rectangle  . Its length and width are
. Its length and width are


so its area is the product of these, or
 .
.
The length and width of Rectangle  are
are


so its area is the product of these, or
 .
.
We want to know what percent 117 is of 240, which can be answered as follows:

The pink region is Rectangle 
so its area is the product of these, or

The length and width of Rectangle 
so its area is the product of these, or

We want to know what percent 117 is of 240, which can be answered as follows:
← Didn't Know|Knew It →

Note: Figure NOT drawn to scale
Refer to the above diagram.
40% of Rectangle  is pink.
is pink.  .
.
Evaluate  .
.

Note: Figure NOT drawn to scale
Refer to the above diagram.
40% of Rectangle 

Evaluate 
Tap to reveal answer
Rectangle  has length
has length  and width
and width  , so it has area
, so it has area
 .
.
300 is 40% of, or 0.40 times, the area of Rectangle  , which we will call
, which we will call  . We can determine
. We can determine  as follows:
as follows:

 .
.
The length of Rectangle  is
is
 ,
,
so its width is
 .
.
Since
 ,
,


Rectangle 



300 is 40% of, or 0.40 times, the area of Rectangle 



The length of Rectangle 

so its width is

Since

← Didn't Know|Knew It →

Note: Figure NOT drawn to scale

What percent of Rectangle  is white?
is white?

Note: Figure NOT drawn to scale
What percent of Rectangle 
Tap to reveal answer
The pink region is Rectangle  . Its length and width are
. Its length and width are


so its area is the product of these, or
 .
.
The length and width of Rectangle  are
are


so its area is the product of these, or
 .
.
The white region is Rectangle  cut from Rectangle
cut from Rectangle  , so its area is the difference of the two:
, so its area is the difference of the two:
 .
.
So we want to know what percent 162 is of 450, which can be answered as follows:

The pink region is Rectangle 
so its area is the product of these, or

The length and width of Rectangle 
so its area is the product of these, or

The white region is Rectangle 


So we want to know what percent 162 is of 450, which can be answered as follows:
← Didn't Know|Knew It →

Note: Figure NOT drawn to scale

Give the ratio of the perimeter of Rectangle  to that of Rectangle
to that of Rectangle  .
.

Note: Figure NOT drawn to scale
Give the ratio of the perimeter of Rectangle 

Tap to reveal answer
The perimeter of Rectangle  is
is

Opposite sides of a rectangle are congruent, so

and

The perimeter of Rectangle  is
is

Opposite sides of a rectangle are congruent, so
 ,
,
 ,
,
and

The ratio of the perimeters is
 - that is, 7 to 5.
- that is, 7 to 5.
The perimeter of Rectangle 
Opposite sides of a rectangle are congruent, so
and
The perimeter of Rectangle 
Opposite sides of a rectangle are congruent, so


and
The ratio of the perimeters is

← Didn't Know|Knew It →

Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in orange). The dirt path is seven feet wide throughout. Which of the following polynomials gives the area of the dirt path in square feet?

Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in orange). The dirt path is seven feet wide throughout. Which of the following polynomials gives the area of the dirt path in square feet?
Tap to reveal answer
The area of the dirt path is the difference between the areas of the outer and inner rectangles.
The outer rectangle has area

The area of the inner rectangle can be found as follows:
The length of the garden is  feet less than that of the entire lot, or
feet less than that of the entire lot, or
 ;
;
The width of the garden is  less than that of the entire lot, or
less than that of the entire lot, or
 ;
;
The area of the garden is their product:




Now, subtract the areas:

The area of the dirt path is the difference between the areas of the outer and inner rectangles.
The outer rectangle has area
The area of the inner rectangle can be found as follows:
The length of the garden is 

The width of the garden is 

The area of the garden is their product:
Now, subtract the areas:
← Didn't Know|Knew It →
If the area of a square is  units squared, what is the length of its diagonal?
units squared, what is the length of its diagonal?
If the area of a square is 
Tap to reveal answer
The diagonal of a square creates two special 45-45-90 triangles, meaning that the diagonal of a square is just the length of one side of the square multiplied by the square root of 2.
In this problem, you can figure out the length of one side of the square by finding the square root of the area (which is equal to a side length), then multiplying that number by the square root of 2.


The diagonal of a square creates two special 45-45-90 triangles, meaning that the diagonal of a square is just the length of one side of the square multiplied by the square root of 2.
In this problem, you can figure out the length of one side of the square by finding the square root of the area (which is equal to a side length), then multiplying that number by the square root of 2.
← Didn't Know|Knew It →
A contractor is going to re-tile a rectangular section of the kitchen floor. If the floor is 6ft x 3ft, and he is going to use square tiles with a side of 9in. How many tiles will be needed?
A contractor is going to re-tile a rectangular section of the kitchen floor. If the floor is 6ft x 3ft, and he is going to use square tiles with a side of 9in. How many tiles will be needed?
Tap to reveal answer
We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)
We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)
← Didn't Know|Knew It →





