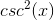Sum and Difference Identities
Help Questions
Pre-Calculus › Sum and Difference Identities
Find the value of 
Explanation
To solve 
Write the formula for these identities.
To solve for 

Substitute the special angles in the formula.
Evaluate both conditions.
Solve for 
Evaluate

Explanation



We can use the sum identity to evaluate this sine:
From the unit circle, we can determine these measures:
Find the value of 
Explanation
To solve 
Write the formula for these identities.
To solve for 

Substitute the special angles in the formula.
Evaluate both conditions.
Solve for 
Find 
Explanation
Using the sum formula for sine,
where,

yeilds:

Find 
Explanation
Using the sum formula for sine,
where,

yeilds:

Evaluate

Explanation



We can use the sum identity to evaluate this sine:
From the unit circle, we can determine these measures:
In the problem below, 

Find

Explanation
Since 




So 
Since 




So 
Using the sine sum formula, we see:
In the problem below, 

Find

Explanation
Since 




So 
Since 




So 
Using the sine sum formula, we see:
According to the trigonometric identities,
Explanation
The trigonometric identity 
Some other identities that are important to know are:
According to the trigonometric identities,
Explanation
The trigonometric identity 
Some other identities that are important to know are:













![=\frac{\sqrt6}{4}+\frac{\sqrt2}{4}-\left[\frac{\sqrt6}{4}-\frac{\sqrt2}{4}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/342878/gif.latex)