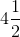Two-Step Equations with Fractions

Help Questions

Pre-Algebra › Two-Step Equations with Fractions

Questions 1 - 10

1

Solve for :

$\frac{1}{2}x+\frac{3}{4}=9$

$16\frac{1}{2}$

$16\frac{1}{4}$

$4\frac{1}{2}$

$16\frac{3}{4}$

Explanation

The goal is to isolate the variable on one side.

$\frac{1}{2}x+\frac{3}{4}=9$

Subtract $\frac{3}{4 }$ from each side of the equation:

$\frac{1}{2}x+\frac{3}{4}-\frac{3}{4}=9-\frac{3}{4}$

$\frac{1}{2}x=8\frac{1}{4}$

Multiply both sides by :

$x=16\frac{1}{2}$

2

Solve for :

$\frac{2}{3}x+6\frac{1}{3}=10\frac{1}{3}$

Explanation

The goal is to isolate the variable to one side.

$\frac{2}{3}x+6\frac{1}{3}=10\frac{1}{3}$

First, convert mixed numbers to improper fractions:

$\frac{2}{3}x+\frac{19}{3}=\frac{31}{3}$

Subtract $\frac{19}{3}$ from both sides:

$\frac{2}{3}x+\frac{19}{3}-\frac{19}{3}=\frac{31}{3}-\frac{19}{3}$

$\frac{2}{3}x=\frac{12}{3}$

Multiply each side by the reciprocal of $\frac{2}{3}$ :

$\frac{3}{2}*\frac{2}{3}x=\frac{12}{3}*\frac{3}{2}$

Cross out like terms and multiply:

$\frac{1}{1}x=\frac{6}{1}*\frac{1}{1}$

3

Solve for x:

$x-\frac{1}{4}=\frac{1}{2}$

$x=\frac{3}{4}$

$x=\frac{3}{2}$

$x=\frac{3}{8}$

$x=-\frac{1}{4}$

Explanation

Once you've isolated x, it's important to find the lowest common denominator so that you can add the two fractions you're working with.

Step 1: Isolate x and convert fractions so that they have a common denominator

$x-\frac{1}{4}+\frac{1}{4}=\frac{1}{2}+\frac{1}{4}$

$x=\frac{1}{2}+ \frac{1}{4}=\frac{1\cdot 2}{2\cdot 2} +\frac{1}{4}=\frac{2}{4}+\frac{1}{4}$

Step 2: solve for x

$x=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}, x=\frac{3}{4}$

4

Solve for :

$1\frac{1}{3}x+7\frac{1}{3}=15\frac{1}{3}$

$6\frac{1}{3}$

$6\frac{2}{3}$

Explanation

Explanation:

The goal is to isolate the variable to one side.

$1\frac{1}{3}x+7\frac{1}{3}=15\frac{1}{3}$

First, convert the mixed numbers to improper fractions:

$\frac{4}{3}x+\frac{22}{3}=\frac{46}{3}$

Subtract $\frac{22}{3}$ from both sides:

$\frac{4}{3}x+\frac{22}{3}-\frac{22}{3}=\frac{46}{3}-\frac{22}{3}$

$\frac{4}{3}x=\frac{24}{3}$

Multiply each side by the reciprocal of $\frac{3}{4}$ :

$\frac{3}{4}*\frac{4}{3}x=\frac{24}{3}*\frac{3}{4}$

5

Solve: $\frac{3}{x} = \frac{1}{6}$

$\frac{1}{2}$

$\frac{1}{18}$

Explanation

Multiply by on both sides of the equation.

$\frac{3}{x} \times x = \frac{1}{6} \times x$

$3 = \frac{x}{6}$

Multiply by on both sides.

$3 \times 6 = \frac{x}{6} \times 6$

6

Solve: $\frac{3}{4}x +\frac{3}{4}= \frac{7}{8}$

$\frac{1}{6}$

$\frac{5}{2}$

$\frac{1}{2}$

$\frac{8}{21}$

Explanation

Subtract $\frac{3}{4}$ on both sides of the equation.

$\frac{3}{4}x +\frac{3}{4}-\frac{3}{4}= \frac{7}{8}-\frac{3}{4}$

Simplify the left side of the equation.

$\frac{3}{4}x= \frac{7}{8}-\frac{3}{4}$

The numerators on the right side of the equation cannot be subtracted unless both denominators are the same. The least common denominator is . Multiply both the numerator and denominator of $\frac{3}{4}$ by two to get the common denominator.

$\frac{3}{4}x= \frac{7}{8}-\frac{3(2)}{4(2)}$

$\frac{3}{4}x= \frac{7}{8}-\frac{6}{8}$

Subtract the numerators on the right side of the equation.

$\frac{3}{4}x= \frac{1}{8}$

Multiply the reciprocal of $\frac{3}{4}$ , or $\frac{4}{3}$ , in order to isolate .

$\frac{3}{4}x \times \frac{4}{3}= \frac{1}{8}\times \frac{4}{3}$

Simplify both sides.

$x= \frac{1}{8}\times \frac{4}{3} = \frac{4}{24} = \frac{1}{6}$

7

Solve: $\frac{4}{x} = 16$

$\frac{1}{4}$

$\frac{1}{64}$

$\frac{1}{20}$

Explanation

In order to solve the equation, we have to isolate the variable. We do this by performing the same operation to either side of the equation.

To isolate , multiply by by both sides on the equation.

$\frac{4}{x} \times x= 16\times x$

Divide by 16 on both sides of the equation.

$\frac{4}{16}=\frac{16x}{16}$

$x=\frac{4}{16}=\frac{1}{4}$

8

Solve for :

$\frac{2}{3}x-\frac{4}{3}=\frac{5}{3}$

$x=\frac{9}{2}$

$x=\frac{2}{9}$

$x=\frac{23}{6}$

$x=\frac{6}{23}$

None of the other answers.

Explanation

$\frac{2}{3}x-\frac{4}{3}=\frac{5}{3}$

Start by isolating the fraction attached the x variable:

$\frac{2}{3}x{\color{Red} -\frac{4}{3}+\frac{4}{3}}=\frac{5}{3}+\frac{4}{3}$

The red terms cancel out.

We add the right side as usual.

$\frac{2}{3}x=\frac{9}{3}$

Reduce fractions where able and multiply by the reciprocal to isolate x:

${\color{Red} \frac{3}{2}*\frac{2}{3}}x=\frac{9}{3}*\frac{3}{2}$

The red terms cancel to 1 and the right is multiplied as usual.

$x=\frac{9}{2}$

9

$8 \left(\frac{1}{2}x + 6\right) = 24$

Explanation

$8 \left(\frac{1}{2}x + 6\right) = 24$

Use the distributive Property first to distribute the eight to both terms within the parentheses.

$\left(8 * \frac{1}{2}x\right) + (8 * 6) = 24$

Simplify from here.

First subtract 48 from both sides.

Now divide by four to isolate and solve for x.

$\frac{4x}{4} = \frac{-24}{4}$

10

Solve for ""

$\frac{1}{2}x -8=4x-1$

Explanation

1.) Add 8 to both sides, removing the "". It now reads $\frac{1}{2}x=4x+7$

2.) Multiply both sides by 2, removing the $\frac{1}{2}$ . It now reads

3.) Subtract from both sides, removing the "". It now reads

4.) Divide both sides by "", resulting in

Page 1 of 4

Return to subject