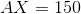Pre-Algebra - Area of a Parallelogram

Find the area of a parallelogram with a base of length 8 and a height of length 6.

Explanation

The area of a parallelogram is

Find the area of a parallelogram if the base is 3 inches and the height is 8 inches.

$24 \textup{ inches} ^2$

$24 \textup{ inches}$

$12 \textup{ inches} ^2$

$576\textup{ inches}^2$

$6 \textup{ inches} ^2$

Explanation

Write the formula for the area of a parallelogram.

Substitute the dimensions.

$A= (3 \textup{ inches})(8\textup{ inches}) = 24 \textup{ inches} ^2$

Find the area of a parallelogram if the base is 13 and the height is 9.

Explanation

Write the formula for the area of a parallelogram.

Substitute the base and height into the equation.

When multiplying two integers first multiply the ones place from each integer:

$9\cdot 3=27$

The seven will stay in the ones place but the two will be carried over. Now multiply the one integer with the tens integer and add the carried over term to that:

The eleven represents the hundreds and tens spot. To get the final answer combine the ones digit to the hundreds and tens digit:

Parallelogram

Note: Figure NOT drawn to scale.

Refer to the above figure, which shows Parallelogram . You are given that $\overline{AX} \perp \overline{BC}$ and $\overline{AY} \perp \overline{CD}$ .

, . .

Evaluate .

$AX = 66\frac{2}{3}$

Explanation

The area of a parallelogram is the product of the length of any one side, or its base, and the length of a segment perpendicular to that side, or its height.

One way to find the area is to multiply the length of side $\overline{CD}$ by its corresponding altitude, $\overline{AY}$ . Since and ,

$A = (CD)(AY) = 120 \cdot 80 = 9,600$ .

Another way to find the area is to multiply the length of side $\overline{BC}$ by its corresponding altitude, $\overline{AX}$ . Since and the area is 9,600, we set up this equation and solve for :

$100 \cdot AX =9,600$

Solve for the area of a parallelogram if the base is and the height is .

Explanation

Write the formula for the area of a parallelogram.

$A=\textup{ Base} \times \textup{ Height}$

Substitute the base and the height into the equation.

The area of the parallelogram is .

Determine the area of a parallelogram with a base and height of $3\sqrt{5}$ .

Explanation

Write the formula to find the area of a parallelogram. Substitute the dimensions.

$A=bh = (3\sqrt5)(3\sqrt5) = 3\times 3\times 5 = 45$

The length of the shorter diagonal of a rhombus is 40% that of the longer diagonal. The area of the rhombus is . Give the length of the longer diagonal in terms of .

$\sqrt{5K}$

$\sqrt{\frac{5K}{2}}$

$K\sqrt{\frac{5}{2}}$

$\frac{1}{5}\sqrt{K}$

$K\sqrt{\frac{2}{5}}$

Explanation

Let be the length of the longer diagonal. Then the shorter diagonal has length 40% of this. Since 40% is equal to $\frac{40}{100 } = \frac{40 \div 20 }{100 \div 20 } = \frac{2}{5}$ , 40% of is equal to $\frac{2}{5}D$ .

The area of a rhombus is half the product of the lengths of its diagonals, so we can set up, and solve for , in the equation:

$\frac{1}{2} \cdot \frac{2}{5}D \cdot D = K$

$\frac{1}{5}D^{2}= K$

$5\cdot \frac{1}{5}D^{2}=5\cdot K$

$D^{2}=5K$

$D =\sqrt{5K}$

A parallelogram has a base length of which is 3 times longer than its corresponding altitude. The area of the parallelogram is 12 square inches. Give the .

$6\sqrt{2}$

$6\sqrt{3}$

Explanation

Base length is so the corresponding altitude is $\frac{t}{3}$ .

The area of a parallelogram is given by:

Where:

is the length of any base
is the corresponding altitude

So we can write:

$12=t\times \frac{t}{3}\Rightarrow t\times t=12\times 3\Rightarrow t^2=36\Rightarrow t=6$

$t\times t=12\times 3$

$t^{2}=36$

Find the area:

Question_5

$\small 24$

$\small 32$

$\small 12$

$\small 16$

Explanation

The area of a parallelogram can be determined using the following equation:

$\small A=bh$

Therefore,

$\small A=8\times3=24$

Parallelogram

Refer to the above figure, which shows Parallelogram . You are given that $\overline{AX} \perp \overline{BC}$ and $\overline{AY} \perp \overline{CD}$ .

If you know the length of $\overline{AD}$ , then, of the following segments, choose the one whose length, if known, will allow us to calculate the area of Parallelogram .

$\overline{AX}$

$\overline{AB}$

$\overline{AY}$

$\overline{CD}$

$\overline{BC}$

Explanation

The area of a parallelogram is the product of the length of any one side, or its base, and the perpendicular distance to the opposite side, or its height. If we know $\overline{AD}$ , then we also know $\overline{BC}$ , which is of the same length. We can take $\overline{BC}$ to be the base, and the segement perpendicular to it, $\overline{AX}$ , as the altitude. Therefore, $\overline{AX}$ is the segment whose length we need to know.

Area of a Parallelogram

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation