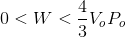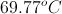To answer this question, it's important to remember how work is defined when dealing with volume and pressure.

The equation for the work done by a gas on its surrounding is as follows.

With this equation in mind, we can see that the only time work is performed is when there is a change in volume. Since we're told in the question stem that the volume remains constant as the pressure is increased, the final volume will be equal to the initial volume. Thus, the term will be equal to and no work will be performed.

The volume of air in the balloon will increase when exposed to hotter temperatures, and decrease when exposed to colder temperatures. If we look at the ideal gas law, we can see that temperature and volume have a direct relationship. As one goes down, so does the other, assuming all other factors remain constant.

We can also look at Charles's law of volumes:

The balloon is sealed, so the amount of gas in the balloon will not change, and the elasticity of the balloon means that pressure will also remain constant. As temperature decreases, volume must also decrease. Suppose that the temperature is halved in our question. The result would be half the volume, according to Charles's law.

By this logic, we can conclude that the balloon will shrink when placed in the cold water.

In this question, we're told that an ideal gas undergoes a change in its temperature and volume, and we're asked to determine how its pressure changes.

First, we'll need to recall the ideal gas equation.

Then, we can rearrange to isolate the term for pressure.

From this expression, we can see that if we double the volume, the pressure will double. Also, cutting the volume in half would double the pressure as well. Therefore, doing both of these would cause the pressure to increase by a factor of .

In this question, we're told the process that a gas takes through various changes in conditions. From this information, we're asked to find a true statement regarding the work done by the gas in this process.

At its initial point, we can define the gas as having an initial pressure and volume as .

First, we're told that the gas goes through an isothermal expansion to triple its volume. Recall that an isothermal process is one in which the temperature of the gas doesn't change. Moreover, because we're dealing with an ideal gas, we can see from the ideal gas equation that a constant temperature means that a changing volume must by accompanied by a change in pressure. Since the volume is being increased by a factor of three, we know that the pressure must be decreasing by a factor of three. Thus, right after the isothermal expansion has finished, the gas will have a pressure and volume of .

Next, we're told that the gas undergoes an isobaric contraction back to its original volume. Thus, we know from this that the pressure won't change, but the volume will return to its original value. Consequently, once the isobaric contraction has come to completion, the gas will have a pressure and volume of .

Finally, we're told that the last process is an isochoric increase of the pressure back to its original amount. Isochoric means that the volume doesn't change in this process. Hence, the gas will now be returned to its original pressure and volume of .

If we were to show this on a pressure vs. volume curve, it would look like the following.

Remember that any pressure-volume work done by a gas is the area under the curve of a pressure vs. volume diagram. For a cyclic process, as the one in this problem, the work done by the gas will be the area within the above image.

For this problem, we don't need to calculate the exact amount of work done. Instead, we can get a rough estimate by first realizing that the structure shown in the above diagram is close to forming a right triangle, but it is slightly smaller. Thus, if we can use the left and bottom sides of the image above to calculate the area that would be enclosed by a right triangle, we can infer that the work done in this problem will be slightly less than the calculated area.

The area for a triangle is the following.

So, for the image shown above, the bottom length is and the side length is . With these values, the area of a right triangle can be calculated.

Finally, since this represents the area for a right triangle, we know that the actual work done is less than this. Hence, the correct answer is:

In this question, we're told that an ideal gas undergoes a change in its temperature and volume, and we're asked to determine how its pressure changes.

First, we'll need to recall the ideal gas equation.

Then, we can rearrange to isolate the term for pressure.

From this expression, we can see that if we double the volume, the pressure will double. Also, cutting the volume in half would double the pressure as well. Therefore, doing both of these would cause the pressure to increase by a factor of .

In this question, we're told the process that a gas takes through various changes in conditions. From this information, we're asked to find a true statement regarding the work done by the gas in this process.

At its initial point, we can define the gas as having an initial pressure and volume as .

First, we're told that the gas goes through an isothermal expansion to triple its volume. Recall that an isothermal process is one in which the temperature of the gas doesn't change. Moreover, because we're dealing with an ideal gas, we can see from the ideal gas equation that a constant temperature means that a changing volume must by accompanied by a change in pressure. Since the volume is being increased by a factor of three, we know that the pressure must be decreasing by a factor of three. Thus, right after the isothermal expansion has finished, the gas will have a pressure and volume of .

Next, we're told that the gas undergoes an isobaric contraction back to its original volume. Thus, we know from this that the pressure won't change, but the volume will return to its original value. Consequently, once the isobaric contraction has come to completion, the gas will have a pressure and volume of .

Finally, we're told that the last process is an isochoric increase of the pressure back to its original amount. Isochoric means that the volume doesn't change in this process. Hence, the gas will now be returned to its original pressure and volume of .

If we were to show this on a pressure vs. volume curve, it would look like the following.

Remember that any pressure-volume work done by a gas is the area under the curve of a pressure vs. volume diagram. For a cyclic process, as the one in this problem, the work done by the gas will be the area within the above image.

For this problem, we don't need to calculate the exact amount of work done. Instead, we can get a rough estimate by first realizing that the structure shown in the above diagram is close to forming a right triangle, but it is slightly smaller. Thus, if we can use the left and bottom sides of the image above to calculate the area that would be enclosed by a right triangle, we can infer that the work done in this problem will be slightly less than the calculated area.

The area for a triangle is the following.

So, for the image shown above, the bottom length is and the side length is . With these values, the area of a right triangle can be calculated.

Finally, since this represents the area for a right triangle, we know that the actual work done is less than this. Hence, the correct answer is:

To answer this question, it's important to remember how work is defined when dealing with volume and pressure.

The equation for the work done by a gas on its surrounding is as follows.

With this equation in mind, we can see that the only time work is performed is when there is a change in volume. Since we're told in the question stem that the volume remains constant as the pressure is increased, the final volume will be equal to the initial volume. Thus, the term will be equal to and no work will be performed.

• We must account for two separate processes since the ice is melting and then warming. The basic formula to calculate the change in entropy at a constant temperature when the ice melts is:

Where is the change in entropy, is the change in heat energy, and is the temperature at which the change of state for the ice occurs. Now we substitute in an equation for for when ice melts: . Our entropy equation now becomes:

Now we plug in our known values into the equation:

Mass

Latent heat of fusion

Temperature

And we get the change in entropy for the ice melting at a constant temperature, which is

• Now we need to calculate the change in entropy for the liquid water warming from to .

The basic formula to calculate the change in entropy at a changing temperature when the water warms is:

Next we substitute in an equation for when there is a temperature change, but not a change in state. That equation is: so our entropy equation now becomes:

next we integrate this equation to get:

Next we plug in the values we know and solve for the change in entropy:

Final temperature of water

Initial temperature of water

Specific heat of water

Mass of water

Now we get the change in entropy for the water warming to be

We add our two entropy values together to find the total change in entropy to be:

• We must account for two separate processes since the ice is melting and then warming. The basic formula to calculate the change in entropy at a constant temperature when the ice melts is:

Where is the change in entropy, is the change in heat energy, and is the temperature at which the change of state for the ice occurs. Now we substitute in an equation for for when ice melts: . Our entropy equation now becomes:

Now we plug in our known values into the equation:

Mass

Latent heat of fusion

Temperature

And we get the change in entropy for the ice melting at a constant temperature, which is

• Now we need to calculate the change in entropy for the liquid water warming from to .

The basic formula to calculate the change in entropy at a changing temperature when the water warms is:

Next we substitute in an equation for when there is a temperature change, but not a change in state. That equation is: so our entropy equation now becomes:

next we integrate this equation to get:

Next we plug in the values we know and solve for the change in entropy:

Final temperature of water

Initial temperature of water

Specific heat of water

Mass of water

Now we get the change in entropy for the water warming to be

We add our two entropy values together to find the total change in entropy to be:

The relationship between mass and temperature, when two masses are mixed together, is:

Using the given values for the mass and specific heat of each compound, we can solve for the final temperature.

We need to work to isolate the final temperature.

Distribute into the parenthesis using multiplication.

Combine like terms.