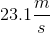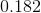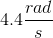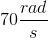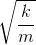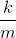Mechanics
Help Questions
Physics › Mechanics
A toy car is set up on a frictionless track containing a downward sloping ramp and a vertically oriented loop. Assume the ramp is 
What additional piece of information is necessary to calculate the maximum height of the loop if the car is to complete the loop and continue out the other side?
None
The mass of the car
The exact shape of the loop
The value of
The distance between the end of the ramp and entrance to the loop
Explanation
This is an example of conservation of energy. The car starts at the top of the ramp, at height 



At the bottom of the loop, all of the potential energy will have been converted into kinetic energy.
As the car traverses the loop and rises above the ground, kinetic energy will be converted back into potential energy. The shape of the loop does not matter in this case -- only the vertical distance between the ground and the car.
In the tallest possible loop, all kinetic energy at the bottom is converted to potential energy at the top. This is the maximum height the car can reach -- there is no additional energy left to continue climbing a taller loop. Therefore, the potential energy at the top of the tallest loop we can build is equal to the kinetic energy at the bottom of the loop. But we have already noted that the kinetic energy at the bottom of the loop is equal to the potential energy at the top of the ramp.
Therefore, we set 






How far can a person jump while running at 

Explanation
We know that:
and we are looking for the maximum height (vertical displacement) this person can obtain, so we aren't concerned with 
We can apply the conservation of energy:
Masses cancel, so
Solve for 

so let's plug in what we know

Fluid flows into a pipe with a diameter of 


Explanation
This question tests the concept of the continuity equation which stipulates that at steady state the volume flowing into one end of a pipe must be exactly equal to the volume flowing out of the other end. That is, 
A baseball has a mass of 


Explanation
We are given the mass of the baseball outside of the water. Using the weight equation 


The buoyancy force is the difference of the weight of the baseball when it is in the air and when it is in the water. So subtract the two differences:
Now we use the buoyancy equation:





and we get
Suppose a 


If the tension in the rope is 

Explanation
To solve this problem, we first need to take into account the forces acting in the vertical direction separately from the forces acting in the horizontal direction.
First, let's start with the vertical direction. Here, the only force force acting downward is the weight of the box. There are two forces acting upwards on the box; one is the normal force and the other is the vertical component of the tension in the rope that is pulling the box. Because the box is not moving in the vertical direction, there is no net force. Thus, the sum of these forces is equal to zero.
Next, let's take a look at the forces acting horizontally on the box. Acting to the right of the box is the horizontal component of the tension in the rope. Acting to the left is the frictional force. Because the box is moving to the right, it must have experienced a net force in this direction. Thus, the sum of these horizontally acting forces will equal a net force.
Now, we can take the expression we obtained for the normal force and substitute it into the expression we obtained for the horizontally acting forces.
Now that we've found an expression for the coefficient of kinetic friction, all we need to do is plug in the values given in the question stem to arrive at the answer.
A pendulum is made up of a small 


Explanation
The angular frequency of a simple pendulum is 

For a simple harmonic motion governed by Hooke's Law, 


Explanation
We know that T is the period. The equation for T is 
Solve for 


Which of these forces is identical to a normal force?
All of these
Force that is perpendicular to the surface
The scale weight of a body
The perpendicular force
The contact force
Explanation
All of these are identical to a normal force.
A pendulum is made up of a small 


Explanation
The angular frequency of a simple pendulum is 

A toy car is set up on a frictionless track containing a downward sloping ramp and a vertically oriented loop. Assume the ramp is 
What additional piece of information is necessary to calculate the maximum height of the loop if the car is to complete the loop and continue out the other side?
None
The mass of the car
The exact shape of the loop
The value of
The distance between the end of the ramp and entrance to the loop
Explanation
This is an example of conservation of energy. The car starts at the top of the ramp, at height 



At the bottom of the loop, all of the potential energy will have been converted into kinetic energy.
As the car traverses the loop and rises above the ground, kinetic energy will be converted back into potential energy. The shape of the loop does not matter in this case -- only the vertical distance between the ground and the car.
In the tallest possible loop, all kinetic energy at the bottom is converted to potential energy at the top. This is the maximum height the car can reach -- there is no additional energy left to continue climbing a taller loop. Therefore, the potential energy at the top of the tallest loop we can build is equal to the kinetic energy at the bottom of the loop. But we have already noted that the kinetic energy at the bottom of the loop is equal to the potential energy at the top of the ramp.
Therefore, we set