Energy and Work - Physics
Card 0 of 412
A 
child descends a slide 
high and reaches the bottom with a speed of 
. How much thermal energy due to friction was generated in this process?
A 
We can use conservation of energy to solve this problem. Let us consider the types of energy at the beginning and the end. At the beginning the child has gravitational potential energy at the top of the slide. When the child reaches the bottom, the child has both kinetic energy and thermal energy as some energy was converted to heat because of the friction on the slide.
The law of conservation of energy states that we can set the energy at the beginning equal to the energy at the end.
This 
difference between the 
at the top and the 
at the bottom is the energy lost to friction.
We can use conservation of energy to solve this problem. Let us consider the types of energy at the beginning and the end. At the beginning the child has gravitational potential energy at the top of the slide. When the child reaches the bottom, the child has both kinetic energy and thermal energy as some energy was converted to heat because of the friction on the slide.
The law of conservation of energy states that we can set the energy at the beginning equal to the energy at the end.
This 
Compare your answer with the correct one above
Conceptual
A man stands on a tall ladder of height 
. He leans over a little too far and falls off the ladder. If his mass is 
, what is his velocity right before he hits the ground?
Conceptual
A man stands on a tall ladder of height 
For this problem, use the law of conservation of energy. This states that the total energy before the fall will equal the total energy after the fall. The initial kinetic energy will be zero, and the final potential energy will be zero; thus, the initial non-zero potential energy will be equal to the final non-zero kinetic energy.
From there, expand the equation to include the individual formulas for potential and kinetic energy calculation.
Notice that the mass will cancel out from both sides.
Now we can solve for the final velocity in terms of the initial height.
For this problem, use the law of conservation of energy. This states that the total energy before the fall will equal the total energy after the fall. The initial kinetic energy will be zero, and the final potential energy will be zero; thus, the initial non-zero potential energy will be equal to the final non-zero kinetic energy.
From there, expand the equation to include the individual formulas for potential and kinetic energy calculation.
Notice that the mass will cancel out from both sides.
Now we can solve for the final velocity in terms of the initial height.
Compare your answer with the correct one above
A runner arrives at the bottom of a hill. He runs up the hill with a constant acceleration until he reaches the top, then runs at a steady pace along the top of the hill. When are the kinetic and potential energies of this man at their greatest?
A runner arrives at the bottom of a hill. He runs up the hill with a constant acceleration until he reaches the top, then runs at a steady pace along the top of the hill. When are the kinetic and potential energies of this man at their greatest?
To answer this question, we can address each type of energy separately. There is no conservation of energy in this problem; kinetic energy is not converted to potential energy as the man runs up the hill. Instead, he is accelerating, indicating an outside force that disallows conservation of energy.
First, we will find the maximum potential energy using the equation:
The man's mass and the acceleration of gravity will remain constant. The only changing variable is height. When the height is greatest, the potential energy will be the greatest. We can conclude that the potential energy will thus be greatest at the top of the hill.
Now we will look at the equation for kinetic energy:
The man's mass will remain constant, and the only changing variable will be the velocity. We are told that the man accelerates as he runs up the hill, indicating that his velocity is increasing. This tells us that he will reach a maximum velocity when he reaches the top of the hill, at which point he maintains a steady velocity along the top of the hill. Since kinetic energy is at a maximum when velocity is at a maximum, we can conclude that kinetic energy is greatest at the top of the hill.
To answer this question, we can address each type of energy separately. There is no conservation of energy in this problem; kinetic energy is not converted to potential energy as the man runs up the hill. Instead, he is accelerating, indicating an outside force that disallows conservation of energy.
First, we will find the maximum potential energy using the equation:
The man's mass and the acceleration of gravity will remain constant. The only changing variable is height. When the height is greatest, the potential energy will be the greatest. We can conclude that the potential energy will thus be greatest at the top of the hill.
Now we will look at the equation for kinetic energy:
The man's mass will remain constant, and the only changing variable will be the velocity. We are told that the man accelerates as he runs up the hill, indicating that his velocity is increasing. This tells us that he will reach a maximum velocity when he reaches the top of the hill, at which point he maintains a steady velocity along the top of the hill. Since kinetic energy is at a maximum when velocity is at a maximum, we can conclude that kinetic energy is greatest at the top of the hill.
Compare your answer with the correct one above
Two balls are thrown off a building with the same speed. One is thrown straight up, and one at a 
angle. Which statement is true if air resistance is ignored?
Two balls are thrown off a building with the same speed. One is thrown straight up, and one at a 
We can use conservation of energy to analyze this problem. When both balls are thrown off the building, they both have the same initial gravitational potential energy. Additionally, since both balls are thrown with the same magnitude of the speed, they both have the same kinetic energy. Energy is a scalar quantity and therefore does not have a direction. Therefore it is independent of the path taken.
At the bottom, both balls will have converted all their potential energy and kinetic energy that they started with to kinetic energy at the bottom of the building. Since both started with the same amount of total energy at the beginning, their kinetic energy at the end will also be the same. Since both balls are assumed to have the same mass, their magnitude of their velocity (speed) will be the same as well. However, their velocity will be in different directions because of the way that the ball was launched.
We can use conservation of energy to analyze this problem. When both balls are thrown off the building, they both have the same initial gravitational potential energy. Additionally, since both balls are thrown with the same magnitude of the speed, they both have the same kinetic energy. Energy is a scalar quantity and therefore does not have a direction. Therefore it is independent of the path taken.
At the bottom, both balls will have converted all their potential energy and kinetic energy that they started with to kinetic energy at the bottom of the building. Since both started with the same amount of total energy at the beginning, their kinetic energy at the end will also be the same. Since both balls are assumed to have the same mass, their magnitude of their velocity (speed) will be the same as well. However, their velocity will be in different directions because of the way that the ball was launched.
Compare your answer with the correct one above
Find the minimum initial height 
of the roller coaster if the roller coaster is to complete the 
diameter loop.
Find the minimum initial height 
First, we need to determine how fast the roller coaster must be going at the top of the loop to continue in a circular motion. At the top of the loop, the only force acting on the car is gravity. Therefore the gravitational force must be the cause of the centripetal motion.
We know that the force of gravity is
And the centripetal force equation is
We can set these two equations equal to each other.
Since mass is on both sides of the equation we can cancel it out.
We can rearrange and solve this equation for the velocity.
We can now use the conservation of energy to determine the initial height of the roller coaster. We know at the top of the roller coaster, there is only 
. At the top of the loop of the coaster there is both 
and 
.
Since mass is each factor, we can cancel it out.
The height of the coaster must start at 
.
First, we need to determine how fast the roller coaster must be going at the top of the loop to continue in a circular motion. At the top of the loop, the only force acting on the car is gravity. Therefore the gravitational force must be the cause of the centripetal motion.
We know that the force of gravity is
And the centripetal force equation is
We can set these two equations equal to each other.
Since mass is on both sides of the equation we can cancel it out.
We can rearrange and solve this equation for the velocity.
We can now use the conservation of energy to determine the initial height of the roller coaster. We know at the top of the roller coaster, there is only 
Since mass is each factor, we can cancel it out.
The height of the coaster must start at 
Compare your answer with the correct one above
Laurence throws a 
rock off the edge of a 
tall building at an angle of 
from the horizontal with an initial speed of 
.
.
What is the total mechanical energy in the vertical direction when the rock is released?
Laurence throws a
What is the total mechanical energy in the vertical direction when the rock is released?
Mechanical energy is the sum of potential and kinetic energies.
Since we're only looking at the vertical components, we need to find the initial vertical velocity. This will be used for the vertical component of the kinetic energy. Use the sine function, initial velocity, and angle for this calculation.
Gravitational potential energy only exists in the vertical plane, so we do not need to manipulate the values. Use our vertical velocity, mass, and the height of the building to find the vertical mechanical energy at the point of release.
Mechanical energy is the sum of potential and kinetic energies.
Since we're only looking at the vertical components, we need to find the initial vertical velocity. This will be used for the vertical component of the kinetic energy. Use the sine function, initial velocity, and angle for this calculation.
Gravitational potential energy only exists in the vertical plane, so we do not need to manipulate the values. Use our vertical velocity, mass, and the height of the building to find the vertical mechanical energy at the point of release.
Compare your answer with the correct one above
Laurence throws a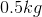 
rock off the edge of a 
tall building at an angle of 
from the horizontal with an initial speed of 
.
.
What is the vertical kinetic energy right before the rock hits the ground?
Laurence throws a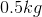
What is the vertical kinetic energy right before the rock hits the ground?
The formula for kinetic energy is:
Since the velocity we're working with is going to be in the vertical direction, we need to find the final 
. The best place to start is by finding the initial vertical velocity. To do that, we need to break the given velocity into its vertical component by using the sine function and the angle.
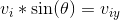
We know that the rock is going to travel a net of 
, as that's the displacement between the rock's initial position (on the building) and the ground. Using the appropriate motion equation, we can find the final velocity using the initial velocity, displacement, and acceleration.
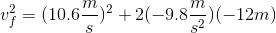
Use this final vertical velocity and the mass of the rock to calculate the final kinetic energy in the vertical direction.
The formula for kinetic energy is:
Since the velocity we're working with is going to be in the vertical direction, we need to find the final
We know that the rock is going to travel a net of
Use this final vertical velocity and the mass of the rock to calculate the final kinetic energy in the vertical direction.
Compare your answer with the correct one above
Sam throws a 
rock off the edge of a 
tall building at an angle of 
from the horizontal. The rock has an initial speed of 
.
What is the total vertical mechanical energy as the rock leaves Sam's hand?
Sam throws a
What is the total vertical mechanical energy as the rock leaves Sam's hand?
Total mechanical energy is the sum of potential energy and mechanical energy.
We can expand this equation to include the formulas for kinetic and potential energy.
Since we are only looking at vertical energies, we need to find the initial vertical velocity to apply toward the kinetic energy.
To find the vertical velocity we use the equation 
.
We can plug in the given values for the angle and initial velocity to solve.
Now we have all the terms necessary to solve for the total energy. Keep in mind that the change in height is going to be negative, since the rock is traveling downward.
Total mechanical energy is the sum of potential energy and mechanical energy.
We can expand this equation to include the formulas for kinetic and potential energy.
Since we are only looking at vertical energies, we need to find the initial vertical velocity to apply toward the kinetic energy.
To find the vertical velocity we use the equation
We can plug in the given values for the angle and initial velocity to solve.
Now we have all the terms necessary to solve for the total energy. Keep in mind that the change in height is going to be negative, since the rock is traveling downward.
Compare your answer with the correct one above
A 
book falls off the top of a 
bookshelf. What is its kinetic energy right before it hits the ground?
A
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
, due to conservation of energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal
Compare your answer with the correct one above
A 
book falls off the top of a 
bookshelf. What is its kinetic energy right before it hits the ground?
A
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is 
.
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal 
, due to conservation of energy.
Remember the law of conservation of energy: the total energy at the beginning equals the total energy at the end. In this case, we have only potential energy at the beginning and only kinetic energy at the end. (The initial velocity is zero, and the final height is zero).
If we can find the potential energy, we can find the kinetic energy. The formula for potential energy is
Using our given values for the mass, height, and gravity, we can solve using multiplication. Note that the height becomes negative because the book is traveling in the downward direction.
The kinetic energy will also equal
Compare your answer with the correct one above
Which of the following is not an example of potential energy?
Which of the following is not an example of potential energy?
The running woman has kinetic energy as she is moving.
The candy bar has chemical potential energy.
The apple has gravitational potential energy.
The rubber band and the spring both have elastic potential energy.
The running woman has kinetic energy as she is moving.
The candy bar has chemical potential energy.
The apple has gravitational potential energy.
The rubber band and the spring both have elastic potential energy.
Compare your answer with the correct one above
A man stands on a tall ladder of height 
. He leans over a little too far and falls off the ladder. If his mass is 
, what is his potential energy right before he falls?
A man stands on a tall ladder of height
The potential energy at a given height it the product of the height, the mass of the object, and the acceleration of gravity.
Potential gravitational energy is given from the equation:
The potential energy at a given height it the product of the height, the mass of the object, and the acceleration of gravity.
Potential gravitational energy is given from the equation:
Compare your answer with the correct one above
A man stands on a tall ladder of height 
. He leans over a little too far and falls off the ladder. If his mass is 
, what is his velocity right before he hits the ground?
A man stands on a tall ladder of height
For this problem, use the law of conservation of energy. This states that the total energy before the fall will equal the total energy after the fall. The initial kinetic energy will be zero, and the final potential energy will be zero; thus, the initial non-zero potential energy will be equal to the final non-zero kinetic energy.
From there, expand the equation to include the individual formulas for potential and kinetic energy calculation.
Notice that the mass will cancel out from both sides.
Now we can solve for the final velocity in terms of the initial height.
For this problem, use the law of conservation of energy. This states that the total energy before the fall will equal the total energy after the fall. The initial kinetic energy will be zero, and the final potential energy will be zero; thus, the initial non-zero potential energy will be equal to the final non-zero kinetic energy.
From there, expand the equation to include the individual formulas for potential and kinetic energy calculation.
Notice that the mass will cancel out from both sides.
Now we can solve for the final velocity in terms of the initial height.
Compare your answer with the correct one above
A ball drops from a height 
. What more do we need to calculate initial potential energy?
A ball drops from a height
The formula for potential energy is:
Since 
is a constant, the acceleration due to gravity on Earth, we only need the mass and the height. The problem gives a height, so we only need mass.
Given the mass and the height, we would be able to calculate the initial potential energy.
The formula for potential energy is:
Since
Given the mass and the height, we would be able to calculate the initial potential energy.
Compare your answer with the correct one above
A runner arrives at the bottom of a hill. He runs up the hill with a constant acceleration until he reaches the top, then runs at a steady pace along the top of the hill. When are the kinetic and potential energies of this man at their greatest?
A runner arrives at the bottom of a hill. He runs up the hill with a constant acceleration until he reaches the top, then runs at a steady pace along the top of the hill. When are the kinetic and potential energies of this man at their greatest?
To answer this question, we can address each type of energy separately. There is no conservation of energy in this problem; kinetic energy is not converted to potential energy as the man runs up the hill. Instead, he is accelerating, indicating an outside force that disallows conservation of energy.
First, we will find the maximum potential energy using the equation:
The man's mass and the acceleration of gravity will remain constant. The only changing variable is height. When the height is greatest, the potential energy will be the greatest. We can conclude that the potential energy will thus be greatest at the top of the hill.
Now we will look at the equation for kinetic energy:
The man's mass will remain constant, and the only changing variable will be the velocity. We are told that the man accelerates as he runs up the hill, indicating that his velocity is increasing. This tells us that he will reach a maximum velocity when he reaches the top of the hill, at which point he maintains a steady velocity along the top of the hill. Since kinetic energy is at a maximum when velocity is at a maximum, we can conclude that kinetic energy is greatest at the top of the hill.
To answer this question, we can address each type of energy separately. There is no conservation of energy in this problem; kinetic energy is not converted to potential energy as the man runs up the hill. Instead, he is accelerating, indicating an outside force that disallows conservation of energy.
First, we will find the maximum potential energy using the equation:
The man's mass and the acceleration of gravity will remain constant. The only changing variable is height. When the height is greatest, the potential energy will be the greatest. We can conclude that the potential energy will thus be greatest at the top of the hill.
Now we will look at the equation for kinetic energy:
The man's mass will remain constant, and the only changing variable will be the velocity. We are told that the man accelerates as he runs up the hill, indicating that his velocity is increasing. This tells us that he will reach a maximum velocity when he reaches the top of the hill, at which point he maintains a steady velocity along the top of the hill. Since kinetic energy is at a maximum when velocity is at a maximum, we can conclude that kinetic energy is greatest at the top of the hill.
Compare your answer with the correct one above
A 
mass is put at the end of a spring with a spring constant of 
. The spring is then compressed 
. What is the maximum velocity of the mass?
A
For this problem, we're going to use the law of conservation of energy. Since we're looking for max velocity, we're going to say that the 
of the system.
The formula for potential energy of a spring is 
Therefore:
Notice that the 
's cancel out.
Plug in our given values.
For this problem, we're going to use the law of conservation of energy. Since we're looking for max velocity, we're going to say that the
The formula for potential energy of a spring is
Therefore:
Notice that the
Plug in our given values.
Compare your answer with the correct one above
A 
box is dropped 
. How much work was done on the box?
A
The formula for work is 
, work equals force times distance.
In this case, there is only one force acting upon the object: the force due to gravity. Plug in our given information for the distance to solve for the work done by gravity.
Remember, since the object will be moving downward, the distance should be negative.
The work done is positive because the distance and the force act in the same direction.
The formula for work is
In this case, there is only one force acting upon the object: the force due to gravity. Plug in our given information for the distance to solve for the work done by gravity.
Remember, since the object will be moving downward, the distance should be negative.
The work done is positive because the distance and the force act in the same direction.
Compare your answer with the correct one above
A 
book falls off the top of a 
bookshelf. How much work is required to lift the book back to its original position, assuming the lifting is done with a constant velocity?
A
Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to 
. The work is thus also equal to 
.
Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to
Compare your answer with the correct one above
A 
book falls off the top of a 
bookshelf. How much work is required to put the book back on the top of the bookshelf, assuming it is lifted with a constant velocity?
A
Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to 
. The work is thus also equal to 
.
Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to
Compare your answer with the correct one above
A 
book falls off the top of a 
bookshelf. How much work is required to put the book back on the top of the bookshelf, assuming it is lifted with a constant velocity?
A
Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to 
. The work is thus also equal to 
.
Work is a force times a distance:
We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:
We can expand the right side of the equation using Newton's second law:
Use the given mass and value of gravity to solve for the lifting force.
Now that we have the force and the distance, we can solve for the work to lift the book.
This problem can also be solved using energy. Work is equal to the change in potential energy:
While on the ground, the book has zero potential energy. Once back on the shelf, the energy is equal to
Compare your answer with the correct one above