Voltage, Energy, and Power
Help Questions
MCAT Physical › Voltage, Energy, and Power
–8 µJ
–2 µJ
2 µJ
8 µJ
16 µJ
Explanation
Given that
V(q) = U
When V is voltage, U is electrical potential energy and q is charge, we can solve by plugging in 4 for V and -2 for q. Also, we must understand that the electric potential energy of a particle decreases as it moves from an area of higher energy to one of lower energy. For an electron, it has higher energy in the negative terminal of the battery than it does in when getting to the positive terminal.
What is the resistance in a wire carrying a voltage of 

Explanation
The formula we can use here is the power formula that involved both resistance and voltage:
We are given the voltage and power, allowing us to solve for the resistance.
A 

Explanation
Electric power is expressed in a number of ways. We will need to use the relationship that involves current and resistance:
We are given the current and resistance, allowing us to calculate the power.
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.

What is the voltage drop across RA?
Explanation
First, we need to determine the voltage drop across R1, and then we can subtract that from the 9V battery to determine the voltage drop across RA. Given that RA and R4 are in parallel, we know that the voltage drop across each is the same.
The voltage drop across R1 can be calculated using the Icircuit (all the current generated by the battery’s potential difference must pass through R1 because it is in direct series with the battery), and the resistance of the resistor.
I can be calculated by V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR allows us to find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25 A
Plugging this value in, we can find the voltage drop across R1.
VR1 = IR = (2.25 A)(2Ω) = 4.5 V
Now we can determine the voltage drop across the parallel resistors by subtracting the voltage drop across R1 from the battery.
VA = 9V – 4.5V = 4.5V
Because RA and R4 are in parallel, the voltage drop across R4 is also 4.5V
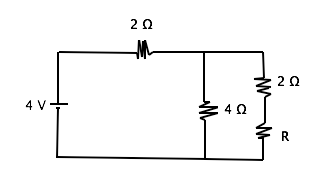
Suppose you have a circuit with two resistors connected in parallel. The first resistor (resistor A) has a resistance of 

Resistor A will have less power dissipation than resistor B
Resistor A will have more power dissipation than resistor B
Resistor A and resistor B will have the same power dissipation
The relative power dissipation in the two resistors cannot be determined from the given information
Explanation
Recall that circuit elements (such as resistors) connected in parallel have the same potential difference; therefore, resistor A and resistor B must have the same potential difference. Since we have information about the potential difference and the resistance of the two resistors, it would be best to use the equation for power in terms of voltage and resistance.
Since the potential difference is constant for both resistors, the power will only depend on the resistance. The equation implies that the power decreases when resistance is high; therefore, resistor A will have lower power dissipation than resistor B because resistor A has the greater resistance.
Household voltage in the United States is 
Explanation
Alternative current (AC) voltage is governed by the RMS (root-mean square) voltage law. This means that the RMS voltage of the circuit will be 
Using the values from our question, we can find the maximum voltage value.
Consider two resistors connected in series. The resistor with more power dissipation will likely have __________ potential difference and __________ resistance than the resistor with less power dissipation.
a larger . . . a smaller
a larger . . . a larger
the same . . . a larger
the same . . . a smaller
Explanation
Resistors connected in series will have the same current flowing through them, but will have different potential differences. Since we are concerned with the differences in potential difference and resistance, we need to use the power dissipation equation in terms of voltage and resistance:
The equation implies that there will be a greater power dissipation when the potential difference increases and the resistance decreases. A resistor undergoing greater power dissipation will most likely have a higher potential difference and lower resistance.
Which of the following is false regarding power dissipation in an electrical circuit?
I. A decrease in power dissipation across a resistor means more of the electrical energy is converted to heat
II. Power dissipation always decreases as the resistance of a resistor increases
III. Electrical power could be measured in units of "volt-amperes"
I and II
III only
II and III
I, II, and III
Explanation
Power dissipation is defined as the ability of a circuit element (such as a resistor) to convert the electrical energy to other forms of energy, such as heat or mechanical energy. This means that a decrease in power dissipation will convert less of the electrical energy to heat and mechanical energy. Statement I is false (and therefore a correct answer choice).
Electrical power can be written in terms of voltage (


Notice that resistance is in the numerator in the first equation and in the denominator in the second equation; therefore, the power doesn’t always decrease when resistance increases. It depends on the equation used to calculate the power. Statement II is false (and therefore a correct answer choice).
Amperes is the unit of current and volts is the unit of voltage; therefore, we need to find the equation for power in terms of voltage and current to determine if power can be measured in volt-amperes. The equation for power in terms of voltage and current is:
Power can be measured in the units of volt-amperes (VA). Statement III is true (and therefore an incorrect answer option).
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.

How much power does the circuit provide?
Explanation
This question asks us about the power of the circuit, meaning the amount of energy per unit time. The power equation is P = IV. V = IR can be substituted in to allow P to be calculated from a number of parameters.
P = IV = I2R = V2/R
To solve for P, we first need the current supplied by the battery.
We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR, we can solve for the current.
V = IR
I = V/R = 9V/4Ω = 2.25A
Now, we can use the current we calculated and the voltage that is dissipated across the circuit to calculate the power.
P = IV = (2.25 A)(9V) = 20.25W
How much electrical energy is lost per hour in a circuit that has a resistor with a resistance of 

Explanation
The question is asking for the amount of energy lost per unit of time; therefore, we need to solve for the power dissipation. We are given the resistance and the voltage. This means that we use the power dissipation equation in terms of resistance and voltage:
Solving for power gives us:
Recall that watts is the SI unit for power, but it can be also written as Joules per second. Since we are solving for Joules lost per hour, we need to convert our units:
This means that 108J of electrical energy is lost every hour due to power dissipation in the resistor.