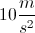MCAT Physical - Motion in Two Dimensions

A projectile is thrown at $80 \frac{m}{s}$ at an angle of 30 degrees. What is the horizontal component of its initial velocity?

${69.3\frac{m}{s}}$

${40.0\frac{m}{s}}$

${58.6\frac{m}{s}}$

${46.9\frac{m}{s}}$

${75.0\frac{m}{s}}$

Explanation

Consider a triangle in which the initial velocity is the hypotenuse. The horizontal component of the velocity can be found using trigonometry:

$v_{ix}=v_i\cos(\theta)$

Use our given values to solve:

$v_{ix}=80\frac{m}{s}\cos(30^{\circ})$

$v_{ix}=69.3\frac{m}{s}$

An object is shot from the ground at 75m/s at an angle of 45⁰ above the horizontal. How high does the object get before beginning its descent?

140m

70m

420m

280m

Explanation

The velocity must be broken down into x (horizontal) and y (vertical) components. We can use the y component to find how high the object gets. To find vertical velocity, vy, use $v_y = v_o sin\theta$ .

$v_y = (75 \frac{m}{s})sin 45^o = 53 \frac{m}{s}$

Next we find how long it takes to reach the top of its trajectory using .

$0 \frac{m}{s} = 53 \frac{m}{s} + (-10 \frac{m}{s^2})t$

t = 5.3s

Finally, find how high the object goes with $d = v_ot +\frac{1}{2}at^{2}$ .

$d = (53\frac{m}{s})5.3s + \frac{1}{2}(-10\frac{m}{s^2})(5.3s)^{2} = 140 m$

A family is on a road trip and travels at 60 mph east for 30 minutes. They miss their exit and turn around, traveling 30 mph west for 6 minutes. What is their total displacement?

$27 \textup{ miles east}$

$30 \textup{ miles east}$

$33 \textup{ miles east}$

$90 \textup{ miles west}$

$60 \textup{ miles west}$

Explanation

Displacement is the change in from intial position to final position. The car first travels 30 miles east and then returns 3 miles west.

East:

$\frac{60mi}{1hr}*0.5hr=30mi$

West:

$\frac{30mi}{1hr}*0.1hr=3mi$

$30\ \text{mi east}-3\ \text{mi west}=27\ \text{mi east}$

They have traveled 27 miles east from their initial position.

Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.

They then decide to sled down the hill, but disagree about who will go first.

Scenario 1:

Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.

Scenario 2:

Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.

Scenario 3:

Unable to agree, Sam and Sally tether themselves with a rope and go down together.

In Scenario 3, before they begin moving, Sam is hanging down the hill facing forward, and Sally has fixed her shoes in the snow to keep her and Sam from beginning down the hill together. If the hill is at a 30o angle to the horizontal, and Sam is stationary but tied to Sally by a rope, how much force does Sam experience down the surface of the hill?

300J

600J

450J

150J

300kJ

Explanation

Sam will experience force down the surface of the inclined plane as per the equation $F=mgsin(\theta)$ .

F = (60kg)(10m/s2) * sin(30o) = 300J

An object is shot from the ground at 125m/s at an angle of 30o above the horizontal. How far away does the object land?

1350m

62.5m

675m

250m

Explanation

First, find the horizontal (x) and vertical (y) components of the velocity

$v_x = v_o cos\theta$

$v_x = (125 \frac{m}{s}) cos(30^o) = 108\frac{m}{s}$

$v_y = v_o sin\theta$

$v_y = (125\frac{m}{s})sin(30^o) = 62.5\frac{m}{s}$

Next, find how long the object is in the air by calculating the time it takes it to reach the top of its path, and doubling that number.

$0 \frac{m}{s} = 62.5 \frac{m}{s} + (-10 \frac{m}{s^2})t$

t = 6.25s

Total time in the air is therefore 12.5s (twice this value).

Finally, find distance traveled my multiplying horizontal velocity and time.

$d_x = 108 \frac{m}{s} (12.5s) = 1,350 m$

A 2kg lead ball is loaded into a spring cannon and the cannon is set at a 45º angle on a platform. The spring has a spring constant of 100N/m and the ball and spring system is compressed by 1m before launch. While the ball is in flight air resistance can be neglected, and the ball finishes its flight by landing at a cushion placed some distance away from the cannon.

What is the initial vertical component of velocity of the ball?

7.1m/s

5.2m/s

7.9m/s

2.3m/s

Explanation

This question also asks us to understand the vector components of velocity. Remember that the final velocity is the hypotenuse of a triangle, and that by knowing the hypotenuse value (solved as 10m/s in a previous problem) we can solve for the vertical component using sine.

vy = (10m/s)(sin(45o)) = 7.1m/s

A 2kg box is at the top of a frictionless ramp at an angle of 60o. The top of the ramp is 30m above the ground. The box is sitting still while at the top of the ramp, and is then released.

What is the velocity of the box just before it hits the ground?

$\small 32.2\frac{m}{s}.$

$\small 37.2\frac{m}{s}.$

$\small 0\frac{m}{s}.$

$\small 22.8\frac{m}{s}.$

Explanation

We can start this problem by determining how much time it takes the box the reach the ground. Since the vertical distance is 30m and we know the angle of the ramp.

$\frac{1}{2}=\frac{30m}{x}\rightarrow x=60m$

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity, using the equation $\small gsin\Theta$ .

$gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}$

We can plug these values into the following distance equation and solve for time.

$\small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}$

$\small 0 = 60 - \frac{1}{2}(8.66)t^{2}$

$\small \small t = 3.72 s$

Now that we know the acceleration on the box and the time of travel, we can use the equation $\small v = v_{0} + at$ to solve for the velocity.

$\small v = 0 + (8.66\frac{m}{s^{2}})(3.72 s) = 32.2 \frac{m}{s}$

A box is placed on a 30o frictionless incline. What is the acceleration of the box as it slides down the incline?

$5\frac{m}{s^2}$

$10\frac{m}{s^2}$

$15\frac{m}{s^2}$

$3\frac{m}{s^2}$

$12\frac{m}{s^2}$

Explanation

To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.

There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30o). Substituting force into F =ma we find that mgsin(30o) = ma. We can now cancel out masses and solve for acceleration.

$F=ma\ and\ F=mgsin(\theta)$

$ma=mgsin(\theta)$

$ma=m(10\frac{m}{s^2})sin(30^o)=m(10\frac{m}{s^2})(0.5)$

$a=5\frac{m}{s^2}$

What is the horizontal acceleration of the ball during its flight?

0m/s2

9.8m/s2

-9.8m/s2

-4.9m/s2

Explanation

Without an additional force acting in the horizontal direction during flight (we are told we can neglect air resistance), there is no acceleration. Remember that Newton's second law, F = ma, requires that a force act on an object to produce acceleration. Here, we have no additional force and thus no acceleration.

How high does the ball fly?

2.57m

5.69m

4.91m

8.50m

Explanation

First, solve for the initial vertical velocity of the ball.

vy = (10m/s)(sin(45o)) = 7.1m/s

Think back to the 3 main kinematics equations we know:

vf2 = vi2 + 2aΔx

vf = vi + at

Δx = vit + ½at2

We need to choose an equation that allows us to solve for the vertical height of the ball, given that we know the initial vertical velocity, final vertical velocity (zero), and the acceleration due to gravity (-9.8m/s2).

vf2 = vi2 + 2aΔy

Δy = (vf2 - vi2)/2a

$\Delta y=\frac{(0\frac{m}{s})^2-(7.1\frac{m}{s})^2}{2(-9.8\frac{m}{s^2})}=2.57m$

Motion in Two Dimensions

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation