Momentum

Help Questions

MCAT Physical › Momentum

Questions 1 - 10

Two astronauts, Ann and Bob, conduct a collision experiment in a weightless, frictionless environment. Initially Ann moves to the right with a momentum of $p_{Ai}=30 \frac{kg*m}{s}$ , and Bob is initially at rest. In the collision, the two astronauts push on each other so that Ann's final momentum is $p_{Af}=-5\frac{kg*m}{s}$ to the left. What is Bob's final momentum?

$35\frac{kg*m}{s}$ to the right

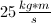
$25\frac{kg*m}{s}$ to the right

$5\frac{kg*m}{s}$ to the right

$5\frac{kg*m}{s}$ to the left

$25\frac{kg*m}{s}$ to the left

Explanation

Apply conservation of momentum before and after the collision.

$p_{Ai}+p_{Bi}=p_{Af}+p_{Bf}$ .

Taking left to be the negative direction, and noting that Bob's initial momentum is 0 since he is at rest, we can use the provided information to see that $30 \frac{kg*m}{s} = -5 \frac{kg*m}{s} + p_{Bf}$ .

Solving for $p_{Bf}$ , we get $p_{Bf}=35 \frac{kg*m}{s}$ . Since this answer is positive, Bob's momentum is in the positive direction (to the right).

Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.

Over the course of the afternoon, they collide many times. Four collisions are described below.

Collision 1:

Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going $5\frac{m}{s}$ and subsequently slides into a stationary child 2. They remain linked together after the collision.

Collision 2:

Child 1 and child 2 are sliding in the same direction. Child 2, moving at $10\frac{m}{s}$ , slides into child 1, moving at $2\frac{m}{s}$ .

Collision 3:

The two children collide while traveling in opposite directions at $10\frac{m}{s}$ each.

Collision 4:

The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of $+8\frac{m}{s}$ .

In all of the above scenarios, which of the following quantities is conserved?

I. Kinetic energy

II. Potential energy

III. Momentum

III only

I and II

II and III

I and III

I, II, and III

Explanation

Kinetic energy and potential energy are interconverted. While total energy is conserved, kinetic energy is allowed to increase or decrease, provided that potential energy does the opposite. For example, as the child in collision 1 is starting at the top of a ramp, she has potential energy, but no kinetic energy. At the bottom of the ramp, all the potential energy has been turned into kinetic energy.

Momentum, on the other hand, is conserved in every collision.

Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.

They then decide to sled down the hill, but disagree about who will go first.

Scenario 1:

Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.

Scenario 2:

Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.

Scenario 3:

Unable to agree, Sam and Sally tether themselves with a rope and go down together.

If the hill is frictionless, what momentum does Sam experience when he reaches the bottom of the 50m hill on his sled in Scenario 1?

1898kg*m/s

60kg*m/s

1581kg*m/s

1340kg*m/s

0kg*m/s

Explanation

The momentum is equal to Sam's total mass times his velocity. His velocity can be found from his potential energy, using conservation of energy. Keep in mind, his total mass includes the mass of his sled.

PE = mgh = (50kg + 10kg) * 10m/s2 * 50m

PE = 30,000J

KE = 30,000J = 1/2mv2 = 1/2(60kg)(v2)

v2 = 1000 m2/s2 = 31.2m/s

p = mv = 60 kg * 31.2 m/s = 1898 kg*m/s

If you had used 30J in place of 30kJ in the KE calculation, you would have chosen 60kg*m/s

A billiard ball moving at $6\frac{m}{s}$ to the right hits a bowling ball at rest. The billiard ball then moves in the opposite direction at $0.25\frac{m}{s}$ .

What is the velocity of the bowling ball after the collision?

$0.48\frac{m}{s}$

$0.25\frac{m}{s}$

$0.12\frac{m}{s}$

$0.52\frac{m}{s}$

$0.60\frac{m}{s}$

Explanation

We can set this up as a conservation of momentum problem. The sum of the initial momentum for each object must equal the sum of the final momentum of each object.

We have two objects and four different velocities. The system must conserve momentum between the time before the collision and after the collision. We are given the mass of each object and their initial velocities.

$(1kg)(6\frac{m}{s}) + (12kg)(0\frac{m}{s}) = (1kg)v_3 + (12kg){v_4}$

$6\frac{kg\cdot m}{s}=(1kg)v_3+(12kg)v_4$

We are given the magnitude of the billiard ball's final velocity, and told that it changes directions, thus becoming negative. Remember that both velocity and momentum are vector quantities.

$6\frac{kg\cdot m}{s} = (1kg)(-0.25\frac{m}{s}) + (12kg){v_4}$

Finally, we can solve of the final velocity of the bowling ball. We can predict that the bowling ball's velocity will be positive since the net initial velocity is positive, and the final billiard ball velocity is negative. The bowling ball must compensate for the negative momentum of the billiard ball.

$6\frac{kg\cdot m}{s} = (-0.25\frac{kg\cdot m}{s}) + (12kg){v_4}$

$6.25\frac{kg\cdot m}{s}=(12kg)v_4$

$v_4=0.52\frac{m}{s}$

Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.

Over the course of the afternoon, they collide many times. Four collisions are described below.

Collision 1:

Collision 2:

Child 1 and child 2 are sliding in the same direction. Child 2, moving at $10\frac{m}{s}$ , slides into child 1, moving at $2\frac{m}{s}$ .

Collision 3:

The two children collide while traveling in opposite directions at $10\frac{m}{s}$ each.

Collision 4:

The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of $+8\frac{m}{s}$ .

In collision 1, with what velocity will the children be traveling after the collision?

Assume that the velocity with which child 1 hits child 2 is the same as the velocity with which child 1 reaches the surface of the lake. Also assume that the original direction of travel for child 1 is positive. Ignore friction and wind resistance.

$2.9\frac{m}{s}$

$-2.9\frac{m}{s}$

$4.1\frac{m}{s}$

$-4.1\frac{m}{s}$

$0\frac{m}{s}$

Explanation

Momentum is always conserved in collisions, and is equal to the product of mass and velocity.

They then decide to sled down the hill, but disagree about who will go first.

Scenario 1:

Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.

Scenario 2:

Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.

Scenario 3:

Unable to agree, Sam and Sally tether themselves with a rope and go down together.

A third boy, John, comes to play on a neighboring hill. Sally goes to play with him, and they find that after they sled down the first hill, Sally was traveling 12m/s. John was only moving at 8m/s. John weighs 80kg with his sled. Which of the following is true?

Sally has lower momentum, John has lower kinetic energy

Sally has greater momentum, John has lower kinetic energy

Sally has greater momentum, while they have roughly equal kinetic energies

Sall has greater momentum, John has greater kinetic energy

Sally has lower momentum, John has greater kinetic energy

Explanation

Kinetic energy emphasizes velocity, by squaring the velocity term.

KE = 1/2mv2

Sally's KE = 1/2(52 kg)(12 m/s)2 = 3,744J

John's KE = 1/2(80 kg)(8m/s)2 = 2,560J

p = mv

Sally's Momentum = 52kg * 12m/s = 624 kg*m/s

John's Momentum = 80kg * 8m/s = 640 kg*m/s

In which of the following collisions is momentum not conserved?

All of the collisions describe situations in which momentum is conserved

A football player tackles another football player travelling in the opposite direction

A star explodes and releases material in several different directions

A bullet is shot at a moving target and becomes embedded upon impact

Two cars travelling in perpendicular directions crash and slide along the asphalt in one piece

Explanation

Momentum is conserved in both elastic and inelastic collisions. During an elastic collision, kinetic energy is also conserved and the two objects remain separate after impact. During an inelastic collision, kinetic energy is lost to the surroundings and the objects traditionally stick together upon impact. The energy lost in an inelastic collision is generally transformed into heat or sound.

The only time momentum will not be conserved is when an outside force is introduced or the masses of objects do not remain constant.

Ball A, traveling $7\frac{m}{s}$ to the right, collides with ball B, traveling $8\frac{m}{s}$ to the left. If ball A is 4kg and ball B is 6kg, what will be the final velocity and direction after a perfectly inelastic collision?

$2\frac{m}{s}\ \text{to the left}$

$5\frac{m}{s}\ \text{to the left}$

$2\frac{m}{s}\ \text{to the right}$

$5\frac{m}{s}\ \text{to the right}$

$6\frac{m}{s}\ \text{to the right}$

Explanation

A perfectly inelastic collision is when the two bodies stick together at the end. At the beginning the two balls are traveling separately with individual momentum values. Using the momentum equation , we can see that ball A has a momentum of (4kg)(7m/s) to the right and ball B has a momentum of (6kg)(8m/s) to the left. The final momentum would be the mass of both balls times the final velocity, (4+6)(vf). We can solve for vf through conservation of momentum; the sum of the initial momentum values must equal the final momentum.

$(4kg)(7m/s) + (6kg)(-8m/s) = (10kg)(v_{f})$

Note: ball B's velocity is negative because they are traveling in opposite directions.

The negative sign indicates the direction in which the two balls are traveling. Since the sign is negative and we indicated that traveling to the left is negative, the two balls must be traveling 2m/s to the left after the perfectly inelastic collision.

Two cars collide in a head-on collision. Afterward, they move together with a net momentum eastward. Which of the following collisions could produce this result?

A car travels eastward at $20\frac{m}{s}$ , and hits a traveling westward at $30\frac{m}{s}$

A car travels westward at $20\frac{m}{s}$ , and hits a traveling westward at $30\frac{m}{s}$

A car travels westward at $20\frac{m}{s}$ , and hits a traveling eastward at $30\frac{m}{s}$

A car travels eastward at $10\frac{m}{s}$ , and hits a traveling westward at $20\frac{m}{s}$

A car travels eastward at $20\frac{m}{s}$ , and hits a traveling westward at $30\frac{m}{s}$

Explanation

The momentum formula is . We know that momentum is conserved during the collision, and that the final momentum must be eastward; thus, the initial net momentum must also be eastward, since momentum is a vector. Only one answer choice gives an eastward (positive) momentum.

Answer possibilities:

$(1500kg)(-20\frac{m}{s})+(900kg)(-30\frac{m}{s})=-57000\frac{kg\cdot m}{s}$

$(1500kg)(-20\frac{m}{s})+(900kg)(30\frac{m}{s})=-3000\frac{kg\cdot m}{s}$

$(1500kg)(10\frac{m}{s})+(900kg)(-20\frac{m}{s})=-3000\frac{kg\cdot m}{s}$

$(1500kg)(20\frac{m}{s})+(1000kg)(-30\frac{m}{s})=0\frac{kg\cdot m}{s}$

$(1500kg)(20\frac{m}{s})+(900kg)(-30\frac{m}{s})=3000\frac{kg\cdot m}{s}$

A 200-gram object moves in the +x direction at 4m/s and collides with an identical object moving in the –y direction at 3m/s. If the two objects stick together after the collision, what is the magnitude of their resulting velocity?

2.5m/s

3.5m/s

5m/s

7m/s

6.5m/s