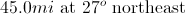To solve this question, you must understand the difference between total distance and total displacement. While it is true that the baseball traveled a specific distance, the displacement is the final position of the baseball relative to the original position of the ball. The ball started and ended in the same place, so its total displacement is 0m.

Near the earth's surface (neglecting air resistance), all objects in free-fall accelerate downwards at . This occurs even when the object's velocity is zero, for example when it is at the top of its flight.

At maximum height, the projectile is still moving in the x-direction. The horizontal component of velocity remains constant during projectile motion, therefore .

Gravity is always acting on any body in projectile motion, therefore . Acceleration will be constant at .

At its peak height, the ball will have a velocity of ; however, the acceleration on the ball due to gravity is constantly experienced by the baseball. As a result, while in the air, the ball will always have a vertical acceleration of

It is stated that between seconds 3 and 6 the object's acceleration increases. On a velocity vs. time graph, this would translate into a nonlinear curve.

Between seconds 1 and 3 the acceleration is constant, and would result in a linear velocity-time relationship. When the object travels at a constant velocity, the acceleration, which correlates to the slope, is zero.

Use the equation to find the distance traveled in each part of the trip.

Part 1 (east):

Part 2 (north):

Part 3 (east):

Find the total distance traveled in each direction.

Treat these components as sides of a right triangle, in which the hypotenuse represents the total displacement. Find the hypotenuse of this triangle using the Pythagorean theorem.

Now that we have the magnitude of the displacement, we still need to find the directional angle. The angle north of east can be found with an inverse trigonometry function, such as inverse tangent. We know that we are working with a triangle with sides of north and east, and the hypotenuse equal to the displacement. Orienting the angle, we can see that the opposite side is the northwards displacement, and the adjacent side is the eastwards displacement.

The average velocity is equal to displacement over time.

The displacement of the race car is zero because the ending position was the same as the starting position. The average velocity will therefore also be equal to zero.

Remember that velocity is a vector, while speed is a scalar. Velocity is measured in terms of displacement and speed is measured in terms of distance.

Choice 3 is correct. Recall that physics problems tell you where to begin and end. The only thing that matters in figuring displacement is the beginning point and end point. The man effectively walked along the hypotenuse of a right triangle whose sides measured 2 km each. Since a2 + b2 = c2, then 4 + 4 = c2, and the correct response is the square root of 8 with the direction of the displacement added for clarity.

Inconstant velocity implies a non-zero acceleration. A non-zero acceleration implies a non-zero force.

Circular motion is made possible by acceleration along the radius of the circle. Since there is acceleration, the linear velocity is not constant even if angular velocity is constant.

The other scenarios describe instances in which there is no net force, and thus no net acceleration or change in velocity.

Choice 4 is correct. In physics, it is often helpful to draw a diagram of the problem. In this case, the respondent would draw a vector 10 hours x 10 knots from south to north (usually going towards the top of a sheet of paper) and a perpendicular vector 50 nautical miles long projecting from the arrowhead of the first vector to the left, or west. The hypotenuse of the right triangle so created is the actual path of a boat experiencing these forces. Without resorting to calculating the square root of the sum of (10,000 plus 2,500 nautical miles2), it is obvious that choice 4 is the only reasonable one.