Magnetic Forces and Energy - MCAT Physical
Card 0 of 42
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a  charge travelling at a constant velocity of
charge travelling at a constant velocity of  through a perpendicular
through a perpendicular  magnetic field?
magnetic field?
What is the magnitude of force on a 


The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
Compare your answer with the correct one above
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume  is 90o.
is 90o.
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume 
The force of a charge in a magnetic field is given by the equation  . q is the charge, v is the velocity, and B is the magnetic field strength.
. q is the charge, v is the velocity, and B is the magnetic field strength.
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation  . I is the current, L is the length or the wire, and B is the magnetic field strength.
. I is the current, L is the length or the wire, and B is the magnetic field strength.
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation  .
.
By manipulating the variables, we can generate the equation  . None of the other answer choices can be derived from these equations.
. None of the other answer choices can be derived from these equations.
The force of a charge in a magnetic field is given by the equation 
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation 
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation 
By manipulating the variables, we can generate the equation 
Compare your answer with the correct one above
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:

This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
Compare your answer with the correct one above

The particle depicted above on the left has a charge of  and a velocity
and a velocity  going to the right. What will happen when the particle enters the magnetic field depicted?
going to the right. What will happen when the particle enters the magnetic field depicted?

The particle depicted above on the left has a charge of 

To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist  clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist 
Compare your answer with the correct one above
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a  charge travelling at a constant velocity of
charge travelling at a constant velocity of  through a perpendicular
through a perpendicular  magnetic field?
magnetic field?
What is the magnitude of force on a 


The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
Compare your answer with the correct one above
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume  is 90o.
is 90o.
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume 
The force of a charge in a magnetic field is given by the equation  . q is the charge, v is the velocity, and B is the magnetic field strength.
. q is the charge, v is the velocity, and B is the magnetic field strength.
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation  . I is the current, L is the length or the wire, and B is the magnetic field strength.
. I is the current, L is the length or the wire, and B is the magnetic field strength.
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation  .
.
By manipulating the variables, we can generate the equation  . None of the other answer choices can be derived from these equations.
. None of the other answer choices can be derived from these equations.
The force of a charge in a magnetic field is given by the equation 
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation 
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation 
By manipulating the variables, we can generate the equation 
Compare your answer with the correct one above
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:

This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
Compare your answer with the correct one above

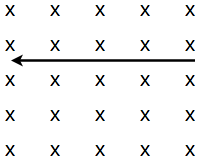
The particle depicted above on the left has a charge of  and a velocity
and a velocity  going to the right. What will happen when the particle enters the magnetic field depicted?
going to the right. What will happen when the particle enters the magnetic field depicted?

The particle depicted above on the left has a charge of 

To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist  clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist 
Compare your answer with the correct one above
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a  charge travelling at a constant velocity of
charge travelling at a constant velocity of  through a perpendicular
through a perpendicular  magnetic field?
magnetic field?
What is the magnitude of force on a 


The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle enters a uniform magnetic field, with velocity v perpendicular to the field, and moves in a circular path of radius R. If the particle's mass were doubled, the radius would become __________.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
A charged particle's motion in a uniform magnetic field is described by R = mv/qB, so the radius of the particle's path is proportional to its mass. Thus if mass is doubled, radius is also doubled.
Compare your answer with the correct one above
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume  is 90o.
is 90o.
In a current-carrying wire, which of the following expressions best relates charge, current, velocity and the length of the wire?
Assume 
The force of a charge in a magnetic field is given by the equation  . q is the charge, v is the velocity, and B is the magnetic field strength.
. q is the charge, v is the velocity, and B is the magnetic field strength.
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation  . I is the current, L is the length or the wire, and B is the magnetic field strength.
. I is the current, L is the length or the wire, and B is the magnetic field strength.
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation  .
.
By manipulating the variables, we can generate the equation  . None of the other answer choices can be derived from these equations.
. None of the other answer choices can be derived from these equations.
The force of a charge in a magnetic field is given by the equation 
Additionally, the force on a current-carrying carrying wire in a magnetic field is given by the equation 
Because we assume the angle to be 90o , we can set the two force equations equal to each other, and derive the equation 
By manipulating the variables, we can generate the equation 
Compare your answer with the correct one above
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
An electron is moving at a constant velocity due east. It travels from a region of zero magnetic field into a uniform magnetic field of nonzero magnitude and unknown direction. Which of the following could not describe the electron's motion after entering the field?
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:

This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
A magnetic force can accelerate a charged particle by changing the direction of its velocity, but cannot change the magnitude of velocity.
If the magnetic field has any components perpendicular to the particle's initial velocity, the particle will experience a force according to the equation:
This force is generated perpendicular to the particle's path and will cause a change in the direction of the particle's velocity. If the magnetic field is parallel to the initial velocity, the particle will experience no magnetic force, and its path will remain unchanged. It is not possible for the particle to accelerate in the magnetic field without changing direction.
Compare your answer with the correct one above

The particle depicted above on the left has a charge of  and a velocity
and a velocity  going to the right. What will happen when the particle enters the magnetic field depicted?
going to the right. What will happen when the particle enters the magnetic field depicted?

The particle depicted above on the left has a charge of 

To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist  clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
clockwise so that your thumb is in the direction of the velocity of the charge. Next, extend your index finger so you are pointing into the plane of the page/screen with it, with your palm facing up. Now rotate your wrist so your index finger points in the direction of the magnetic field lines. Now your index finger should be pointing down, with your palm facing the screen/page, and your thumb still pointing to the right. The direction of the magnetic force felt by a positive charge is perpendicularly from your palm outwards, into the plane of the page/screen. Note that if the charge were negative, the direction of the magnetic force felt by the charge would be coming perpendicularly from the top of your hand instead.
To determine the direction the charge will accelerate, use the right hand rule for magnetic force. To begin, hold out your hand and give a "thumb up," now rotate your wrist 
Compare your answer with the correct one above
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
When finding the direction of the force on a POSITIVELY charged particle due to a magnetic field, we can use the right hand rule. Holding your thumb perpendicular to the rest of your fingers (as if motioning to stop), orient your fingers parallel to the lines of the magnetic field, and your thumb with the velocity vector of the charge. For a positive charge, the force would be oriented directly out of the palm; HOWEVER, the charge of an electron is negative and therefore the force will be applied in the opposite direction. This would mean that the force would be coming directly out of the backside of your hand (in this case, towards the top of the page) using the right hand rule.
Compare your answer with the correct one above
What is the magnitude of force on a  charge travelling at a constant velocity of
charge travelling at a constant velocity of  through a perpendicular
through a perpendicular  magnetic field?
magnetic field?
What is the magnitude of force on a 


The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
The equation for finding the force on a charge in a magnetic field is
F = qvBsinθ
Where q is charge in coulombs, v is the velocity of the charge, and B is the strength of the magnetic field in Teslas. Since the charge is moving perpendicular to the magnetic field, sinθ =1. Therefore we solve for force by plugging in the values and multiplying.
Compare your answer with the correct one above