Identifying Slope at a Point - Math
Card 1 of 4
Find the slope of the line tangent to the  -intercept of the parabola:
-intercept of the parabola:

Find the slope of the line tangent to the 
Tap to reveal answer
To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the  -coordinate of the specific point in the new equation.
-coordinate of the specific point in the new equation.
In this case, it helps to expand the equation before taking the derivative:

Now take the derivative of the expanded equation:

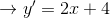
Since the  -intercept is the point where the
-intercept is the point where the  -coordinate is
-coordinate is  , substitute
, substitute  into the equation for
into the equation for  .
.

To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the 
In this case, it helps to expand the equation before taking the derivative:
Now take the derivative of the expanded equation:
Since the 



← Didn't Know|Knew It →
Find the slope of the line tangent to the  -intercept of the parabola:
-intercept of the parabola:

Find the slope of the line tangent to the 
Tap to reveal answer
To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the  -coordinate of the specific point in the new equation.
-coordinate of the specific point in the new equation.
In this case, it helps to expand the equation before taking the derivative:

Now take the derivative of the expanded equation:

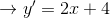
Since the  -intercept is the point where the
-intercept is the point where the 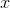 -coordinate is
-coordinate is  , substitute
, substitute  into the equation for
into the equation for  .
.

To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the 
In this case, it helps to expand the equation before taking the derivative:
Now take the derivative of the expanded equation:
Since the 
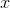



← Didn't Know|Knew It →
Find the slope of the line tangent to the  -intercept of the parabola:
-intercept of the parabola:

Find the slope of the line tangent to the 
Tap to reveal answer
To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the  -coordinate of the specific point in the new equation.
-coordinate of the specific point in the new equation.
In this case, it helps to expand the equation before taking the derivative:

Now take the derivative of the expanded equation:

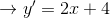
Since the  -intercept is the point where the
-intercept is the point where the 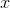 -coordinate is
-coordinate is  , substitute
, substitute  into the equation for
into the equation for  .
.

To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the 
In this case, it helps to expand the equation before taking the derivative:
Now take the derivative of the expanded equation:
Since the 



← Didn't Know|Knew It →
Find the slope of the line tangent to the  -intercept of the parabola:
-intercept of the parabola:

Find the slope of the line tangent to the 
Tap to reveal answer
To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the  -coordinate of the specific point in the new equation.
-coordinate of the specific point in the new equation.
In this case, it helps to expand the equation before taking the derivative:

Now take the derivative of the expanded equation:

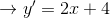
Since the  -intercept is the point where the
-intercept is the point where the 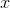 -coordinate is
-coordinate is  , substitute
, substitute  into the equation for
into the equation for  .
.

To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation, then substitute the 
In this case, it helps to expand the equation before taking the derivative:
Now take the derivative of the expanded equation:
Since the 



← Didn't Know|Knew It →