How to solve two-step equations with integers in pre-algebra - Math

Card 0 of 328

Question

Simplify:

$2x^{5} + 5x^5$

Answer

According to the laws of exponents, if you add you do not add the exponents. Therefore , and the variable term remains $x^{5}$ . The answer is .

Compare your answer with the correct one above

Question

Answer

This is a two-step equation. First simplify the whole numbers by adding 6 to both sides:

$24+\left ( 6\right )=2X-6+\left ( 6\right )$

Then divide both sides by 2

$\frac{30}{2}=\frac{2X}{2}$

Compare your answer with the correct one above

Question

Solve for :

Answer

We have two steps to this problem. Remember our end result is to get isolated on one side of the equation.

First we add to each side, cancelling out the on the left side. This brings the equation to .

Remember to get rid of a number we perform the opposite operation. The is multiplied with the , therefore to cancel it out we will divide by .

divided by equals . What we do to one side we must do to the other, therefore we divide by also. This becomes .

Compare your answer with the correct one above

Question

Simplify:

$(2x^{2}+5) (3x^{3}+ 3)$

Answer

The requires the FOIL method (first, outside, inside, last).

Multiplying the first two monomials $2x^2 \cdot 3x^3$ equals $6x^{5}$ .

The outside two are $2x^{2} \cdot 3$ which equals $6x^{2}$ .

The two inside monomials are $5 \cdot 3x^3$ which equals .

The last two are $5\cdot 3$ which is .

All together this becomes $6x^{5}+15x^{3}+6x^{2}+15$ .

Compare your answer with the correct one above

Question

What is if ?

Answer

Plugging in for gives .

=

= .

Compare your answer with the correct one above

Question

Solve the following equation for .

Answer

To solve a two step equation, we want to isolate the variable. This means first "getting rid of" the number which is being added to the variable, in this case . To get rid of the , we first recognize that it is being added, then we do the inverse and subtract from both sides.

Now, we want to do the inverse of multiplying by , which is dividing by on both sides.

$\frac{3m}{3}=\frac{12}{3}$

Compare your answer with the correct one above

Question

Solve the following equation for .

$8 - \frac{k}{7} = 5$

Answer

$8 - \frac{k}{7} = 5$

We want to first isolate the variable, thus we first try to get rid of the constants being added to the variable, in this case the . To eliminate , we do the inverse of addition, and subtract from both sides.

$8-\frac{k}{7}-8=5-8$

$- \frac{k}{7} = -3$

Then, we want to do the inverse of dividing by , which is multiplying by . Remember that multiplying two negative terms results in a positive term.

$(-7)(-\frac{k}{7})=(-7)(-3)$

Compare your answer with the correct one above

Question

Solve for .

Answer

Perform the same operation on both sides of the equation.

Add 3 to both sides.

Divide both sides by 4 and simplify the fraction.

$\frac{4x}{4}=\frac{16}{4}$

Compare your answer with the correct one above

Question

Solve the equation for .

$\small 7p+3=10p$

Answer

$\small 7p+3=10p$

Subtract from both sides to get the variables on the same side, and simplify.

$\small 7p+3-7p=10p-7p$

$\small 3=3p$

Divide both sides by .

$\small \frac{3}{3}=\frac{3p}{3}$

$\small 1=p$

Compare your answer with the correct one above

Question

Solve for $\small s$ .

Answer

Add $\small s$ to both sides.

Subtract 13 from both sides.

Compare your answer with the correct one above

Question

Solve for $\small n$ .

Answer

Subtract 14 from each side.

Divide both sides by 6.

$\frac{6n}{6}=\frac{24}{6}$

Compare your answer with the correct one above

Question

Solve for if, $5x^{2}= 245$ .

Answer

To solve for we must get all of the numbers on the other side of the equation of .

When solving a simple two-step equation we must remove the numbers that are interacting with in this order: Addition/Subtraction, Multiplication/Division, Exponents.

To do this in a problem where is being multiplied by a number, we must divide both sides of the equation by the number.

In this case the number is so we divide each side of the equation by to make it look like this $\frac{5x^{2}}{5}= \frac{245}{5}$

Our new problem will look like this $x^{2}=49$ .

We then must solve the exponential equation.

To solve an equation with 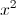we must take the square root of each side of the equation to get 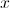by itself.

Doing this makes our problem look like $\sqrt{x^{2}}=\sqrt{49}$

Then we perform the square root to get the answer $x=\pm7$

Remember that $(-7)^{2}$ can also equal so our answer will be both positive and negative.

The final answer looks like $x=\pm7$ .

Compare your answer with the correct one above

Question

Solve for if,

Answer

To perform a two step algebra problem with addition and multiplication we must remove the numbers from so it is by itself on one side of the equation.

To do this we first look to see if a number is being added or subtracted from .

In this case a number is being added so we must subtract the number, , from each side of the equation

Perform the math so our equation looks becomes

Then we divide each side of the equation by the number that is in front of , , to get by itself

$\frac{5x}{5}=\frac{40}{5}$

Perform the math to find the answer

Compare your answer with the correct one above

Question

Solve for if,

Answer

To perform a two-step algebra problem with addition and multiplication we must remove the numbers from so it is by itself on one side of the equation.

To do this we first look to see if a number is being added or subtracted from .

In this case a number is being added so we must subtract the number, , from each side of the equation

Perform the math so our equation becomes

Then we divide each side of the equation by the number that is in front of , , to get by itself $\frac{9x}{9}=\frac{81}{9}$

Perform the math to find the answer

Compare your answer with the correct one above

Question

Solve for if

Answer

To perform a two-step algebra problem with addition and multiplication we must remove the numbers from so it is by itself on one side of the equation.

To do this we first look to see if a number is being added or subtracted from .

In this case a number is being added so we must subtract the number, , from each side of the equation:

Perform the math so that our equation becomes .

Then we divide each side of the equation by the number that is in front of , , to get by itself

$\frac{3x}{3}=\frac{24}{3}$

Perform the math to find the answer

Compare your answer with the correct one above

Question

Solve for if

$\frac{x}{4}-34=6$

Answer

To perform a two-step algebra problem with addition and division we must remove the numbers from so it is by itself on one side of the equation.

To do this we first look to see if a number is being added or subtracted from .

In this case a number is being subtracted so we must add the number, , to each side of the equation

$\frac{x}{4}-34+34=6+34$

Perform the math so our equation becomes

$\frac{x}{4}=40$

Then we multiply each side of the equation by the number that is under , , to get by itself $x=4\cdot 40$

Perform the math to find the answer

Compare your answer with the correct one above

Question

Solve for if

$\frac{x}{7}-64=-32$

Answer

To perform a two step algebra problem with addition and division we must remove the numbers from so it is by itself on one side of the equation.

To do this we first look to see if a number is being added or subtracted from .

In this case a number is being subtracted so we must add the number, , to each side of the equation

$\frac{x}{7}-64+64=-32+64$

Perform the math so our equation becomes

$\frac{x}{7}=32$

Then we multiply each side of the equation by the number that is under to get by itself

$7\cdot \left(\frac{x}{7}\right)=7\cdot (32)$

Perform the math to find the answer

Compare your answer with the correct one above

Question

Solve for if

$\frac{x}{2}-15=75$

Answer

To perform a two-step algebra problem with addition and division we must remove the numbers from so it is by itself on one side of the equation.

To do this we first look to see if a number is being added or subtracted from .

In this case a number is being subtracted so we must add the number, , to each side of the equation

$\frac{x}{2}-15+15=75+15$

Perform the math so our equation becomes

$\frac{x}{2}=90$

Then we multiply each side of the equation by the number that is under to get by itself

$2\cdot \left(\frac{x}{2}\right)=(90)\cdot 2$

Perform the math to find the answer

Compare your answer with the correct one above

Question

Solve for if

Answer

The problem above is a two-step algebra problem with distribution.

To solve you must first distribute the outside of the parentheses to both of the numbers inside my multiplying.

Perform the multiplication with and each of the individual numbers to get our new equation,

Then we must get our variable, , by itself.

We must subtract the number, , from each side of the equation

Perform the math so our equation becomes .

Then we divide each side of the equation by the number that is in front of to get by itself

$\frac{3x}{3}=\frac{30}{3}$

Solve to find the answer .

Compare your answer with the correct one above

Question

Solve for if

Answer

The problem above is a two-step algebra problem with distribution.

To solve you must first distribute the outside of the parentheses into both of the numbers inside my multiplying

Then we must get our variable, , by itself.

To do this we must add the number, , to each side of the equation

Perform the math so our equation becomes .

Then we divide each side of the equation by the number that is in front of to get by itself

$\frac{4x}{4}=\frac{48}{4}$

Perform the math to find the answer

Compare your answer with the correct one above

Tap the card to reveal the answer