How to find the angle for a percentage of a circle - Math
Card 1 of 76

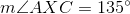 ;
; 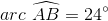 ;
; 
Find the degree measure of  .
.

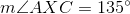
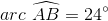
Find the degree measure of 
Tap to reveal answer
When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,

Since  and
and  form a linear pair,
form a linear pair,  , and
, and  .
.
Substitute  and
and  into the first equation:
into the first equation:
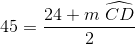


When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,
Since 



Substitute 

← Didn't Know|Knew It →
A sector comprises 20% of a circle. What is the central angle of the sector?
A sector comprises 20% of a circle. What is the central angle of the sector?
Tap to reveal answer
Proporations can be used to solve for the central angle. Let 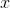 equal the angle of the sector.
equal the angle of the sector.

Cross mulitply:

Solve for  :
:

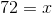
Proporations can be used to solve for the central angle. Let 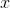
Cross mulitply:
Solve for 
← Didn't Know|Knew It →
How many degrees are in  of a circle?
of a circle?
How many degrees are in 
Tap to reveal answer
There are  degrees in a circleso the equation to solve becomes a simple percentage problem:
degrees in a circleso the equation to solve becomes a simple percentage problem:

There are 
← Didn't Know|Knew It →
A sector contains  of a circle. What is the measure of the central angle of the sector?
of a circle. What is the measure of the central angle of the sector?
A sector contains 
Tap to reveal answer
An entire circle is  . A sector that is
. A sector that is  of the circle therefore has a central angle that is
of the circle therefore has a central angle that is  of
of  .
.

Therefore, our central angle is 
An entire circle is 



Therefore, our central angle is
← Didn't Know|Knew It →
If you have  percent of a circle, what is the angle, in degrees, that creates that region?
percent of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
Now you need to convert  into a decimal.
into a decimal.

If you multiply 360 by 0.667, you get the degree measure that corresponds to the percentage, which is 240.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
Now you need to convert 
If you multiply 360 by 0.667, you get the degree measure that corresponds to the percentage, which is 240.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert  into a decimal.
into a decimal.

If you multiply 360 by 0.20, you get the degree measure that corresponds to the percentage, which is 72.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert 
If you multiply 360 by 0.20, you get the degree measure that corresponds to the percentage, which is 72.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
In order to start this problem we need to convert the percent into a decimal.

If you multiply 360 by 0.30, you get the degree measure that corresponds to the percentage, which is 108.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
In order to start this problem we need to convert the percent into a decimal.
If you multiply 360 by 0.30, you get the degree measure that corresponds to the percentage, which is 108.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percent to decimal.

Now if you multiply 360 by 0.35, you get the degree measure that corresponds to the percentage, which is 126.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percent to decimal.
Now if you multiply 360 by 0.35, you get the degree measure that corresponds to the percentage, which is 126.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percentage into a decimal.

If you multiply 360 by 0.90, you get the degree measure that corresponds to the percentage, which is 324.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percentage into a decimal.
If you multiply 360 by 0.90, you get the degree measure that corresponds to the percentage, which is 324.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First we need to convert the percentage into a decimal.

If you multiply 360 by 0.45, you get the degree measure that corresponds to the percentage, which is 162.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First we need to convert the percentage into a decimal.
If you multiply 360 by 0.45, you get the degree measure that corresponds to the percentage, which is 162.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
In order to solve this problem we first need to convert the percentage into a decimal.

If you multiply 360 by 0.375, you get the degree measure that corresponds to the percentage, which is 135.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
In order to solve this problem we first need to convert the percentage into a decimal.
If you multiply 360 by 0.375, you get the degree measure that corresponds to the percentage, which is 135.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First we need to convert the percentage into a decimal.

If you multiply 360 by 0.70, you get the degree measure that corresponds to the percentage, which is 252.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First we need to convert the percentage into a decimal.
If you multiply 360 by 0.70, you get the degree measure that corresponds to the percentage, which is 252.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First we need to convert the percentage into a decimal.

If you multiply 360 by 0.80, you get the degree measure that corresponds to the percentage, which is 288.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First we need to convert the percentage into a decimal.
If you multiply 360 by 0.80, you get the degree measure that corresponds to the percentage, which is 288.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percentage into a decimal.

If you multiply 360 by 0.44, you get the degree measure that corresponds to the percentage, which is 158.4.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percentage into a decimal.
If you multiply 360 by 0.44, you get the degree measure that corresponds to the percentage, which is 158.4.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percentage into a decimal.

If you multiply 360 by 0.18, you get the degree measure that corresponds to the percentage, which is 64.8.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
First convert the percentage into a decimal.
If you multiply 360 by 0.18, you get the degree measure that corresponds to the percentage, which is 64.8.
← Didn't Know|Knew It →
If you have  of a circle, what is the angle, in degrees, that creates that region?
of a circle, what is the angle, in degrees, that creates that region?
If you have 
Tap to reveal answer
A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
We first need to convert the percentage into a decimal.

If you multiply 360 by 0.56, you get the degree measure that corresponds to the percentage, which is 201.6.

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.
We first need to convert the percentage into a decimal.
If you multiply 360 by 0.56, you get the degree measure that corresponds to the percentage, which is 201.6.
← Didn't Know|Knew It →

What is the angle measure of  in the figure above if the sector comprises 37% of the circle?
in the figure above if the sector comprises 37% of the circle?

What is the angle measure of 
Tap to reveal answer
It is very easy to compute the angle of a sector if we know what it is as a percentage of the total circle. To do this, you merely need to multiply  by
by  ˚. This yields
˚. This yields  ˚.
˚.
It is very easy to compute the angle of a sector if we know what it is as a percentage of the total circle. To do this, you merely need to multiply 


← Didn't Know|Knew It →

What is the angle measure of  in the figure above if the sector comprises
in the figure above if the sector comprises  % of the circle?
% of the circle?

What is the angle measure of 

Tap to reveal answer
It is very easy to compute the angle of a sector if we know what it is as a percentage of the total circle. To do this, you merely need to multiply  by
by  ˚. This yields
˚. This yields  ˚.
˚.
It is very easy to compute the angle of a sector if we know what it is as a percentage of the total circle. To do this, you merely need to multiply 


← Didn't Know|Knew It →
What is the angle measure of  in the figure if the sector comprises
in the figure if the sector comprises  of the circle?
of the circle?

What is the angle measure of 


Tap to reveal answer
It is very easy to compute the angle of a sector if we know what it is as a percentage of the total circle. To do this, you merely need to multiply  by
by  ˚. This yields
˚. This yields  ˚
˚
It is very easy to compute the angle of a sector if we know what it is as a percentage of the total circle. To do this, you merely need to multiply 


← Didn't Know|Knew It →
How many degrees are in  of a circle?
of a circle?
How many degrees are in 
Tap to reveal answer
There are  degrees in a circleso the equation to solve becomes a simple percentage problem:
degrees in a circleso the equation to solve becomes a simple percentage problem:

There are 
← Didn't Know|Knew It →