Graphing Linear Functions - Math
Card 1 of 148
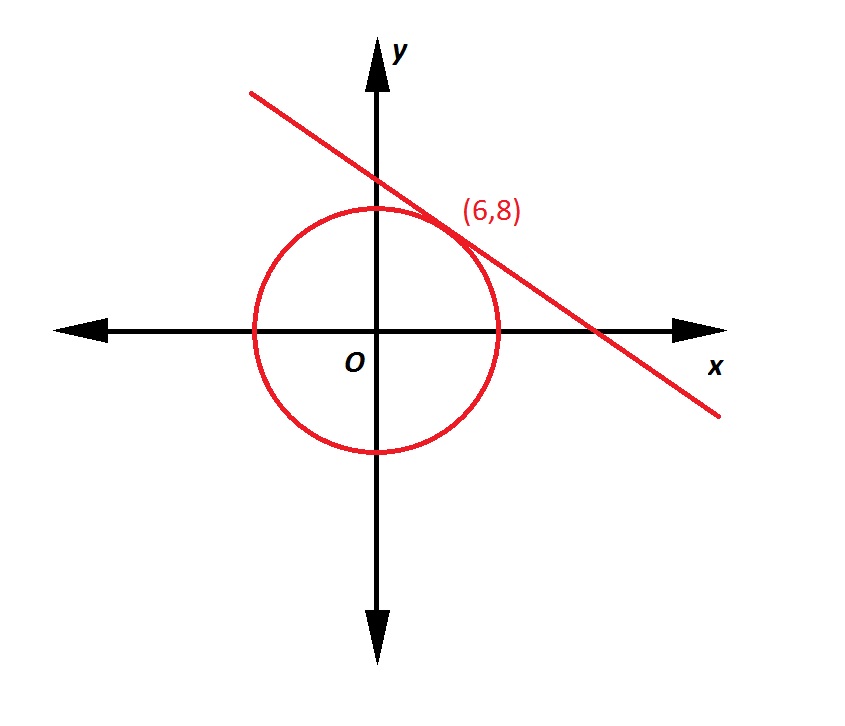
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?

Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Tap to reveal answer
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints  , has slope
, has slope
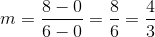 .
.
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be  . Since it includes point
. Since it includes point  , we can use the point-slope form of the line to find its equation:
, we can use the point-slope form of the line to find its equation:

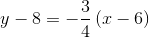

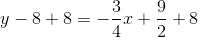

A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
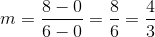
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 

← Didn't Know|Knew It →
Solve:


Solve:
Tap to reveal answer
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







← Didn't Know|Knew It →
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

Tap to reveal answer
To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


← Didn't Know|Knew It →
Solve:


Solve:
Tap to reveal answer
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







← Didn't Know|Knew It →
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

Tap to reveal answer
To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


← Didn't Know|Knew It →

Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?

Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Tap to reveal answer
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints  , has slope
, has slope
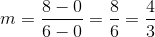 .
.
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be  . Since it includes point
. Since it includes point  , we can use the point-slope form of the line to find its equation:
, we can use the point-slope form of the line to find its equation:

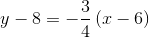

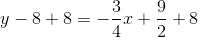

A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
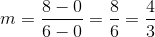
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 

← Didn't Know|Knew It →
Determine where the graphs of the following equations will intersect.


Determine where the graphs of the following equations will intersect.
Tap to reveal answer
We can solve the system of equations using the substitution method.


Solve for  in the second equation.
in the second equation.



Substitute this value of  into the first equation.
into the first equation.

Now we can solve for  .
.




Solve for  using the first equation with this new value of
using the first equation with this new value of  .
.




The solution is the ordered pair  .
.
We can solve the system of equations using the substitution method.
Solve for 
Substitute this value of 
Now we can solve for 
Solve for 

The solution is the ordered pair 
← Didn't Know|Knew It →
Which of the following graphs correctly depicts the graph of the inequality 
Which of the following graphs correctly depicts the graph of the inequality
Tap to reveal answer
Let's start by looking at the given equation:

The inequality is written in slope-intercept form; therefore, the slope is equal to  and the y-intercept is equal to
and the y-intercept is equal to  .
.
All of the graphs depict a line with slope of  and y-intercept
and y-intercept  . Next, we need to decide if we should shade above or below the line. To do this, we can determine if the statement is true using the origin
. Next, we need to decide if we should shade above or below the line. To do this, we can determine if the statement is true using the origin  . If the origin satisfies the inequality, we will know to shade below the line. Substitute the values into the given equation and solve.
. If the origin satisfies the inequality, we will know to shade below the line. Substitute the values into the given equation and solve.


Because this statement is true, the origin must be included in the shaded region, so we shade below the line.
Finally, a statement that is "less than" or "greater than" requires a dashed line in the graph. On the other hand, those that are "greater than or equal to" or "less than or equal to" require a solid line. We will select the graph with shading below a dashed line.
Let's start by looking at the given equation:
The inequality is written in slope-intercept form; therefore, the slope is equal to 

All of the graphs depict a line with slope of 


Because this statement is true, the origin must be included in the shaded region, so we shade below the line.
Finally, a statement that is "less than" or "greater than" requires a dashed line in the graph. On the other hand, those that are "greater than or equal to" or "less than or equal to" require a solid line. We will select the graph with shading below a dashed line.
← Didn't Know|Knew It →

Refer to the above diagram. which of the following compound inequality statements has this set of points as its graph?

Refer to the above diagram. which of the following compound inequality statements has this set of points as its graph?
Tap to reveal answer
A horizontal line has equation  for some value of
for some value of  ; since the line goes through a point with
; since the line goes through a point with  -coordinate 3, the line is
-coordinate 3, the line is  . Also, since the line is solid and the region above this line is shaded in, the corresponding inequality is
. Also, since the line is solid and the region above this line is shaded in, the corresponding inequality is  .
.
A vertical line has equation  for some value of
for some value of  ; since the line goes through a point with
; since the line goes through a point with  -coordinate 4, the line is
-coordinate 4, the line is  . Also, since the line is solid and the region right of this line is shaded in, the corresponding inequality is
. Also, since the line is solid and the region right of this line is shaded in, the corresponding inequality is  .
.
Since only the region belonging to both sets is shaded - that is, their intersection is shaded - the statements are connected with "and". The correct choice is  .
.
A horizontal line has equation 




A vertical line has equation 




Since only the region belonging to both sets is shaded - that is, their intersection is shaded - the statements are connected with "and". The correct choice is 
← Didn't Know|Knew It →

Which of the following inequalities is graphed above?

Which of the following inequalities is graphed above?
Tap to reveal answer
First, we determine the equation of the boundary line. This line includes points  and
and  , so the slope can be calculated as follows:
, so the slope can be calculated as follows:

Since we also know the  -intercept is
-intercept is  , we can substitute
, we can substitute  in the slope-intercept form to obtain equation of the boundary:
in the slope-intercept form to obtain equation of the boundary:


The boundary is excluded, as is indicated by the line being dashed, so the equality symbol is replaced by either  or
or  . To find out which one, we can test a point in the solution set - we will choose
. To find out which one, we can test a point in the solution set - we will choose  :
:








1 is greater than 0 so the correct symbol is 
The inequality is 
First, we determine the equation of the boundary line. This line includes points 

Since we also know the 


The boundary is excluded, as is indicated by the line being dashed, so the equality symbol is replaced by either 






1 is greater than 0 so the correct symbol is
The inequality is
← Didn't Know|Knew It →

Which of the following inequalities is graphed above?

Which of the following inequalities is graphed above?
Tap to reveal answer
First, we determine the equation of the boundary line. This line includes points  and
and  , so the slope can be calculated as follows:
, so the slope can be calculated as follows:

Since we also know the  -intercept is
-intercept is  , we can substitute
, we can substitute  in the slope-intercept form to obtain the equation of the boundary line:
in the slope-intercept form to obtain the equation of the boundary line:


The boundary is included, as is indicated by the line being solid, so the equality symbol is replaced by either  or
or  . To find out which one, we can test a point in the solution set - for ease, we will choose
. To find out which one, we can test a point in the solution set - for ease, we will choose  :
:






0 is less than 3 so the correct symbol is  .
.
The inequality is  .
.
First, we determine the equation of the boundary line. This line includes points 

Since we also know the 


The boundary is included, as is indicated by the line being solid, so the equality symbol is replaced by either 





0 is less than 3 so the correct symbol is 
The inequality is 
← Didn't Know|Knew It →

Which equation best matches the graph of the line shown above?

Which equation best matches the graph of the line shown above?
Tap to reveal answer
To find an equation of a line, we will always need to know the slope of that line -- and to find the slope, we need at least two points. It looks like we have (0, -3) and (12,0), which we'll call point 1 and point 2, respectively.

Now we need to plug in a point on the line into an equation for a line. We can use either slope-intercept form or point-slope form, but since the answer choices are in point-slope form, let's use that.


Unfortunately, that's not one of the answer choices. That's because we didn't pick the same point to substitute into our equation as the answer choices did. But we can see if any of the answer choices are equivalent to what we found. Our equation is equal to:

which is the slope-intercept form of the line. We have to put all the other answer choices into slope-intercept to see if they match. The only one that works is this one:




To find an equation of a line, we will always need to know the slope of that line -- and to find the slope, we need at least two points. It looks like we have (0, -3) and (12,0), which we'll call point 1 and point 2, respectively.
Now we need to plug in a point on the line into an equation for a line. We can use either slope-intercept form or point-slope form, but since the answer choices are in point-slope form, let's use that.
Unfortunately, that's not one of the answer choices. That's because we didn't pick the same point to substitute into our equation as the answer choices did. But we can see if any of the answer choices are equivalent to what we found. Our equation is equal to:
which is the slope-intercept form of the line. We have to put all the other answer choices into slope-intercept to see if they match. The only one that works is this one:
← Didn't Know|Knew It →

What is the equation of the line displayed above?

What is the equation of the line displayed above?
Tap to reveal answer
The equation of a line is  , with m being the slope of the line, and b being the y-intercept. The y intercept of the line is at
, with m being the slope of the line, and b being the y-intercept. The y intercept of the line is at  , so
, so  .
.
The x-intercept is at  , the equation becomes
, the equation becomes  , simplification yields
, simplification yields 
The equation of a line is 


The x-intercept is at 

← Didn't Know|Knew It →

What is the equation of the above line?

What is the equation of the above line?
Tap to reveal answer
The equation of a line is  with m being the slope and b being the y intercept. The y-intercept is at
with m being the slope and b being the y intercept. The y-intercept is at  , so
, so  . The x-intercept is
. The x-intercept is  , so after plugging in the equation becomes
, so after plugging in the equation becomes  , simplifying to
, simplifying to  .
.
The equation of a line is 





← Didn't Know|Knew It →

Refer to the line in the above diagram. It we were to continue to draw it so that it intersects the  -axis, where would its
-axis, where would its  -intercept be?
-intercept be?

Refer to the line in the above diagram. It we were to continue to draw it so that it intersects the 

Tap to reveal answer
First, we need to find the slope of the line.
In order to move from the lower left point to the upper right point, it is necessary to move up five units and right three units. This is a rise of 5 and a run of 3. makes the slope of the line shown  .
.
We can use this to find the  -intercept
-intercept  using the slope formula as follows:
using the slope formula as follows:
The lower left point has coordinates  . Therefore, we can set up and solve for
. Therefore, we can set up and solve for  in this slope formula, setting
in this slope formula, setting  :
:







First, we need to find the slope of the line.
In order to move from the lower left point to the upper right point, it is necessary to move up five units and right three units. This is a rise of 5 and a run of 3. makes the slope of the line shown 
We can use this to find the 

The lower left point has coordinates 


← Didn't Know|Knew It →
Line  includes the points
includes the points  and
and  . Line
. Line  includes the points
includes the points  and
and  . Which of the following statements is true of these lines?
. Which of the following statements is true of these lines?
Line 





Tap to reveal answer
We calculate the slopes of the lines using the slope formula.
The slope of line  is
is

The slope of line  is
is

The lines have the same slope, making them either parallel or identical.
Since the slope of each line is 0, both lines are horizontal, and the equation of each takes the form  , where
, where  is the
is the  -coordinate of each point on the line. Therefore, line
-coordinate of each point on the line. Therefore, line  and line
and line  have equations
have equations  and
and  .This makes them parallel lines.
.This makes them parallel lines.
We calculate the slopes of the lines using the slope formula.
The slope of line 
The slope of line 
The lines have the same slope, making them either parallel or identical.
Since the slope of each line is 0, both lines are horizontal, and the equation of each takes the form 






← Didn't Know|Knew It →
An individual's maximum heart rate can be found by subtracting his or her age from  . Which graph correctly expresses this relationship between years of age and maximum heart rate?
. Which graph correctly expresses this relationship between years of age and maximum heart rate?
An individual's maximum heart rate can be found by subtracting his or her age from 
Tap to reveal answer
In  form, where y = maximum heart rate and x = age, we can express the relationship as:
form, where y = maximum heart rate and x = age, we can express the relationship as:

We are looking for a graph with a slope of -1 and a y-intercept of 220.
The slope is -1 because as you grow one year older, your maximum heart rate decreases by 1.
In 
We are looking for a graph with a slope of -1 and a y-intercept of 220.
The slope is -1 because as you grow one year older, your maximum heart rate decreases by 1.
← Didn't Know|Knew It →
Which of the following is the function graphed below?

Which of the following is the function graphed below?

Tap to reveal answer
This function is linear (a line), so we must remember that we can represent lines algebraically using y=mx+b, where m is the slope and b is the y-intercept.
Looking at the graph, we can tell immediately that the y-intercept is -5, because the line crosses(intercepts) the y-axis at -5.
To find the slope, we need two points,  and the following formula:
and the following formula:
 .
.
For the sake of the example, choose (0,-5) and (2,-1). We can see that the graph clearly passes through each of these points. Any two points will do, however. Substituting each of the values into the slope formula yields m=2.
Thus, our final answer is 
This function is linear (a line), so we must remember that we can represent lines algebraically using y=mx+b, where m is the slope and b is the y-intercept.
Looking at the graph, we can tell immediately that the y-intercept is -5, because the line crosses(intercepts) the y-axis at -5.
To find the slope, we need two points, 

For the sake of the example, choose (0,-5) and (2,-1). We can see that the graph clearly passes through each of these points. Any two points will do, however. Substituting each of the values into the slope formula yields m=2.
Thus, our final answer is
← Didn't Know|Knew It →
Where does  cross the
cross the  axis?
axis?
Where does 

Tap to reveal answer
To find where this equation crosses the  axis or its
axis or its  -intercept, change the equation into slope intercept form.
-intercept, change the equation into slope intercept form.

Subtract to isolate  :
:

Divide both sides by  to completely isolate
to completely isolate  :
:

This form is the slope intercept form  where
where  is the slope of the line and
is the slope of the line and  is the
is the  -intercept.
-intercept.
To find where this equation crosses the 

Subtract to isolate 
Divide both sides by 

This form is the slope intercept form 



← Didn't Know|Knew It →
Select the equation of the line perpendicular to the graph of  .
.
Select the equation of the line perpendicular to the graph of 
Tap to reveal answer
Lines are perpendicular when their slopes are the negative recicprocals of each other such as  . To find the slope of our equation we must change it to slope y-intercept form.
. To find the slope of our equation we must change it to slope y-intercept form.

Subtract the x variable from both sides:

Divide by 4 to isolate y:

The negative reciprocal of the above slope:  . The only equation with this slope is
. The only equation with this slope is  .
.
Lines are perpendicular when their slopes are the negative recicprocals of each other such as 
Subtract the x variable from both sides:
Divide by 4 to isolate y:
The negative reciprocal of the above slope: 

← Didn't Know|Knew It →


