Plane Geometry - Math
Card 0 of 2152
An isosceles triangle has a base of  and an area of
and an area of  . What must be the height of this triangle?
. What must be the height of this triangle?
An isosceles triangle has a base of 

 .
.



Compare your answer with the correct one above
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
Compare your answer with the correct one above
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Compare your answer with the correct one above
A triangle has a perimeter of 36 inches, and one side that is 12 inches long. The lengths of the other two sides have a ratio of 3:5. What is the length of the longest side of the triangle?
A triangle has a perimeter of 36 inches, and one side that is 12 inches long. The lengths of the other two sides have a ratio of 3:5. What is the length of the longest side of the triangle?
We know that the perimeter is 36 inches, and one side is 12. This means, the sum of the lengths of the other two sides are 24. The ratio between the two sides is 3:5, giving a total of 8 parts. We divide the remaining length, 24 inches, by 8 giving us 3. This means each part is 3. We multiply this by the ratio and get 9:15, meaning the longest side is 15 inches.
We know that the perimeter is 36 inches, and one side is 12. This means, the sum of the lengths of the other two sides are 24. The ratio between the two sides is 3:5, giving a total of 8 parts. We divide the remaining length, 24 inches, by 8 giving us 3. This means each part is 3. We multiply this by the ratio and get 9:15, meaning the longest side is 15 inches.
Compare your answer with the correct one above
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
Compare your answer with the correct one above
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
Compare your answer with the correct one above
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
Compare your answer with the correct one above
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Compare your answer with the correct one above
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
Compare your answer with the correct one above
If 2 sides of the triangle are have lengths equal to 8 and 14, what is one possible length of the third side?
If 2 sides of the triangle are have lengths equal to 8 and 14, what is one possible length of the third side?
The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.




The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.
Compare your answer with the correct one above
In  the length of AB is 15 and the length of side AC is 5. What is the least possible integer length of side BC?
the length of AB is 15 and the length of side AC is 5. What is the least possible integer length of side BC?
In 
Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.
Given lengths of two of the sides of the  are 15 and 5. The length of the third side must be greater than 15-5 or 10 and less than 15+5 or 20.
are 15 and 5. The length of the third side must be greater than 15-5 or 10 and less than 15+5 or 20.
The question asks what is the least possible integer length of BC, which would be 11
Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.
Given lengths of two of the sides of the 
The question asks what is the least possible integer length of BC, which would be 11
Compare your answer with the correct one above

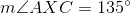 ;
; 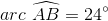 ;
; 
Find the degree measure of  .
.

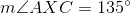
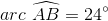
Find the degree measure of 
When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,

Since  and
and  form a linear pair,
form a linear pair,  , and
, and  .
.
Substitute  and
and  into the first equation:
into the first equation:
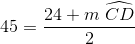


When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,
Since 



Substitute 

Compare your answer with the correct one above
A sector comprises 20% of a circle. What is the central angle of the sector?
A sector comprises 20% of a circle. What is the central angle of the sector?
Proporations can be used to solve for the central angle. Let 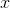 equal the angle of the sector.
equal the angle of the sector.

Cross mulitply:

Solve for  :
:

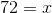
Proporations can be used to solve for the central angle. Let 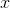
Cross mulitply:
Solve for 
Compare your answer with the correct one above
Two similiar triangles exist where the ratio of perimeters is 4:5 for the smaller to the larger triangle. If the larger triangle has sides of 6, 7, and 12 inches, what is the perimeter, in inches, of the smaller triangle?
Two similiar triangles exist where the ratio of perimeters is 4:5 for the smaller to the larger triangle. If the larger triangle has sides of 6, 7, and 12 inches, what is the perimeter, in inches, of the smaller triangle?
The larger triangle has a perimeter of 25 inches. Therefore, using a 4:5 ratio, the smaller triangle's perimeter will be 20 inches.
The larger triangle has a perimeter of 25 inches. Therefore, using a 4:5 ratio, the smaller triangle's perimeter will be 20 inches.
Compare your answer with the correct one above
If a = 7 and b = 4, which of the following could be the perimeter of the triangle?

I. 11
II. 15
III. 25
If a = 7 and b = 4, which of the following could be the perimeter of the triangle?

I. 11
II. 15
III. 25
Consider the perimeter of a triangle:
P = a + b + c
Since we know a and b, we can find c.
In I:
11 = 7 + 4 + c
11 = 11 + c
c = 0
Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.
In II:
15 = 7 + 4 + c
15 = 11 + c
c = 4.
This is plausible given that the other sides are 7 and 4.
In III:
25 = 7 + 4 + c
25 = 11 + c
c = 14.
It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.
Thus we are left with only II.
Consider the perimeter of a triangle:
P = a + b + c
Since we know a and b, we can find c.
In I:
11 = 7 + 4 + c
11 = 11 + c
c = 0
Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.
In II:
15 = 7 + 4 + c
15 = 11 + c
c = 4.
This is plausible given that the other sides are 7 and 4.
In III:
25 = 7 + 4 + c
25 = 11 + c
c = 14.
It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.
Thus we are left with only II.
Compare your answer with the correct one above
Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?
Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?
The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.
The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.
Compare your answer with the correct one above
Two similiar triangles have a ratio of perimeters of  .
.
If the smaller triangle has sides of 3, 7, and 5, what is the perimeter of the larger triangle.
Two similiar triangles have a ratio of perimeters of 
If the smaller triangle has sides of 3, 7, and 5, what is the perimeter of the larger triangle.
Adding the sides gives a perimeter of 15 for the smaller triangle. Multipying by the given ratio of  , yields 52.5.
, yields 52.5.
Adding the sides gives a perimeter of 15 for the smaller triangle. Multipying by the given ratio of 
Compare your answer with the correct one above
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
Compare your answer with the correct one above
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Compare your answer with the correct one above
If the area of a square is 25 inches squared, what is the perimeter?
If the area of a square is 25 inches squared, what is the perimeter?
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is  or
or  The perimeter of a square is the sum of the length of all 4 sides or
The perimeter of a square is the sum of the length of all 4 sides or 
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is 

Compare your answer with the correct one above