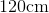ISEE Upper Level Quantitative Reasoning - Hexagons

Find the perimeter of a hexagon with one side having a length of 15cm.

$90\text{cm}$

$120\text{cm}$

$105\text{cm}$

$75\text{cm}$

$135\text{cm}$

Explanation

To find the perimeter of a hexagon, we will use the following formula:

$P = 6 \cdot a$

where a is the length of one side of the hexagon.

Now, we know the length of one side of the hexagon is 15cm.

Knowing this, we can substitute into the formula. We get

$P = 6 \cdot 15\text{cm}$

$P = 90\text{cm}$

A hexagon has six angles with measures $(x-5)^{\circ}, x^{\circ}, (x+5)^{\circ}, (y-10)^{\circ}, y^{\circ}, (y + 10)^{\circ}.$

Which quantity is greater?

(a)

(b) 240

(a) and (b) are equal

(a) is greater

(b) is greater

It is impossible to tell from the information given

Explanation

The angles of a hexagon measure a total of . From the information, we know that:

$3 (x + y) \div 3 = 720 \div 3$

The quantities are equal.

Which is the greater quantity?

(a) The sum of the measures of the exterior angles of a thirty-sided polygon, one per vertex

(b) The sum of the measures of the exterior angles of a forty-sided polygon, one per vertex

(a) and (b) are equal

It is impossible to tell from the information given

(a) is greater

(b) is greater

Explanation

The Polygon Exterior-Angle Theorem states that the sum of the measures of the exterior angles of any polygon, one per vertex, is $360^{\circ }$ . This makes both quantities equal.

A hexagon has six angles with measures $(x-5)^{\circ}, x^{\circ}, (x+5)^{\circ}, (y-10)^{\circ}, y^{\circ}, (y + 10)^{\circ}.$

Which quantity is greater?

(a)

(b) 240

(a) and (b) are equal

(a) is greater

(b) is greater

It is impossible to tell from the information given

Explanation

The angles of a hexagon measure a total of . From the information, we know that:

$3 (x + y) \div 3 = 720 \div 3$

The quantities are equal.

Trapezoid

Figure NOT drawn to scale.

In the above figure, $\overline{XY}$ is the midsegment of isosceles Trapezoid . Also, $TX = \frac{1}{2} XY$ .

What is the perimeter of Trapezoid ?

Explanation

The length of the midsegment of a trapezoid is half sum of the lengths of the bases, so

$XY = \frac{1}{2} (12 + 40) = \frac{1}{2} \cdot 52 = 26$ .

Also, by definition, since Trapezoid is isosceles, . The midsegment divides both legs of Trapezoid into congruent segments; combining these facts:

$TX = XP = \frac{1}{2} TP = \frac{1}{2} RA = RY = YA$

$TX = \frac{1}{2} XY = \frac{1}{2} \cdot 26 = 13$ .

, so the perimeter of Trapezoid is

In a certain quadrilateral, three of the angles are $65^{\circ}$ , $120^{\circ}$ , and $34^{\circ}$ . What is the measure of the fourth angle?

$141^{\circ}$

$139^{\circ}$

$219^{\circ}$

$41^{\circ}$

$29^{\circ}$

Explanation

A quadrilateral has four angles totalling $360^{\circ}$ . So, first add up the three angles given. The sum is $219^{\circ}$ . Then, subtract that from 360. This gives you the missing angle, which is $141^{\circ}$ .

$\Delta ABC$ and $\Delta DEF$ are right triangles, with right angles $\angle B , \angle E$ , respectively.

Which is the greater quantity?

(a) The perimeter of $\Delta ABC$

(b) The perimeter of $\Delta DEF$

It is impossible to tell from the information given.

(a) and (b) are equal.

(a) is greater.

(b) is greater.

Explanation

No information is given about the legs of either triangle; therefore, no information about their perimeters can be deduced.

A rectangle is two feet longer than it is wide; its perimeter is 11 feet. What is its area in square inches?

$945 \textrm{ in}^{2}$

$513 \textrm{ in}^{2}$

$4,212 \textrm{ in}^{2}$

$3,780 \textrm{ in}^{2}$

It is impossible to determine the area from the information given

Explanation

The length of the rectangle is 2 feet, or 24 inches, greater than the width, so, if is the width in inches, is the length in inches.

The perimeter of the rectangle is 11 feet, or $11 \times 12= 132$ inches. The perimeter, in terms of length and width, is , so we can set up the equation: