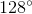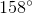ISEE Upper Level Quantitative Reasoning - How to find an angle

$\angle 1$ and $\angle 2$ are supplementary; $\angle 1$ and $\angle 3$ are complementary.

$m \angle 2 = 100 ^{\circ }$ .

What is $m \angle 3$ ?

$10^{\circ }$

$80^{\circ }$

$100^{\circ }$

$50^{\circ }$

Explanation

Supplementary angles and complementary angles have measures totaling $180^{\circ }$ and $90^{\circ }$ , respectively.

$m \angle 2 = 100 ^{\circ }$ , so its supplement $\angle 1$ has measure

$m \angle 1 = 180^{\circ } - m \angle 2 = 180^{\circ } - 100 ^{\circ } = 80^{\circ }$

$\angle 3$ , the complement of $\angle 1$ , has measure

$m \angle 3 = 90^{\circ } - m \angle 1 = 90^{\circ } - 80 ^{\circ } = 10^{\circ }$

Lines

Examine the above diagram. What is ?

Explanation

By angle addition,

$\left ( x - 13\right )+ 100 + (y + 25) = 180$

$x - 13\right+ 100 + y + 25 = 180$

$x + y - 13\right+ 100+ 25 = 180$

Thingy

Note: Figure NOT drawn to scale.

In the above figure, $m \angle 1=\left ( x+17 \right )^{\circ}$ and $m \angle 2= \left (7x+11 \right )^{\circ}$ . Which of the following is equal to $m \angle 1$ ?

$36^{\circ}$

$26^{\circ}$

$7\frac{3}{4}^{\circ }$

$29\frac{5}{7}^{\circ}$

$21\frac{5}{7}^{\circ}$

Explanation

$\angle 1$ and $\angle 2$ form a linear pair, so their angle measures total $180^{\circ}$ . Set up and solve the following equation:

$m \angle 1+ m \angle 2 = 180^{\circ}$

$\left ( x+17 \right ) + \left (7x+11 \right ) = 180$

$m \angle 1=\left ( x+17 \right )^{\circ} = \left ( 19+17 \right )^{\circ} = 36^{\circ}$

Two angles which form a linear pair have measures $(2x+72)^{\circ}$ and $(5x-125)^{\circ}$ . Which is the lesser of the measures (or the common measure) of the two angles?

$41\frac{3}{7}^{\circ}$

$22\frac{6}{7}^{\circ}$

$81\frac{1}{2} ^{\circ }$

$65\frac{2}{3 } ^{\circ }$

$33\frac{2}{7}^{\circ }$

Explanation

Two angles that form a linear pair are supplementary - that is, they have measures that total $180^{\circ}$ . Therefore, we set and solve for in this equation:

$x = \frac{233}{7}= 33 \frac{2}{7}$

The two angles have measure

$2 \cdot 33 \frac{2}{7} +72= 138 \frac{4}{7} ^{\circ}$

and

$5 \cdot 33 \frac{2}{7} -125 = 41\frac{3}{7}^{\circ}$

$41\frac{3}{7}^{\circ}$ is the lesser of the two measures and is the correct choice.

A line intersects parallel lines and . $\angle 1$ and $\angle 2$ are corresponding angles; $\angle 1$ and $\angle 3$ are same side interior angles.

$m \angle 1 = \left (3x+2y \right )^{\circ }$

$m \angle 2 = \left ( 4x+21\right )^{\circ }$

$m \angle 3 = \left ( 2y-27\right )^{\circ}$

Evaluate .

Explanation

When a transversal such as crosses two parallel lines, two corresponding angles - angles in the same relative position to their respective lines - are congruent. Therefore,

Two same-side interior angles are supplementary - that is, their angle measures total 180 - so

We can solve this system by the substitution method as follows:

Backsolve:

, which is the correct response.

Thingy

Figure NOT drawn to scale

The above figure shows Trapezoid , with $\overline{RT}$ and $\overline{RA }$ tangent to the circle. $m \angle T = 106 ^{\circ }$ ; evaluate $m \angle A$ .

$148^{\circ }$

$138^{\circ }$

$128^{\circ }$

$158^{\circ }$

Explanation

By the Same-Side Interior Angle Theorem, since $\overline{TR} || \overline{AP}$ , $\angle T$ and $\angle P$ are supplementary - that is, their degree measures total $180 ^{\circ }$ . Therefore,

$m \angle P + m \angle T = 180 ^{\circ }$

$m \angle P = 180 ^{\circ } - m \angle T$

$m \angle P = 180 ^{\circ } - 106 ^{\circ } = 74^{\circ }$

$\angle P$ is an inscribed angle, so the arc it intercepts, $\overarc{TA}$ , has twice its degree measure;

$m \overarc{TA} = 2 \cdot m \angle P =2 \cdot 74^{\circ } = 148 ^{\circ }$ .

The corresponding major arc, $\overarc{TPA}$ , has as its measure

$m \overarc{TPA} = 360 ^{\circ }- m \overarc{TA} = 360 ^{\circ }- 148 ^{\circ }= 212 ^{\circ }$

The measure of an angle formed by two tangents to a circle is equal to half the difference of those of its intercepted arcs:

$m \angle R = \frac{1}{2} \left (m \overarc{TPA} - m \overarc{TA} \right )$

$m \angle R = \frac{1}{2} \left (212 ^{\circ } -148 ^{\circ } \right )= \frac{1}{2} \cdot 64 ^{\circ } = 32^{\circ }$

Again, by the Same-Side Interior Angles Theorem, $\angle R$ and $\angle A$ are supplementary, so

$m \angle A + m \angle R= 180 ^{\circ }$

$m \angle A = 180 ^{\circ } - m \angle R$

$m \angle A = 180 ^{\circ } - 32 ^{\circ } = 148^{\circ }$

Lines

Examine the above diagram. If $l \parallel m$ , give in terms of .

Explanation

The two marked angles are same-side exterior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for in this equation:

Lines

Examine the above diagram. Which of the following statements must be true whether or not and are parallel?

$\angle 5 \cong \angle 8$

$\angle 5 \cong \angle 4$

$\angle 2 \cong \angle 6$

$m \angle 1 + m \angle 6 = 180 ^{\circ }$

$m \angle 4 + m \angle 7 = 180 ^{\circ }$

Explanation

Four statements can be eliminated by the various parallel theorems and postulates. Congruence of alternate interior angles or corresponding angles forces the lines to be parallel, so

$\angle 5 \cong \angle 4 \Rightarrow l \parallel m$ and

$\angle 2 \cong \angle 6 \Rightarrow l \parallel m$ .

Also, if same-side interior angles or same-side exterior angles are supplementary, the lines are parallel, so

$m \angle 4 + m \angle 7 = 180 ^{\circ } \Rightarrow l \parallel m$ and

$m \angle 1 + m \angle 6 = 180 ^{\circ } \Rightarrow l \parallel m$ .

However, $\angle 5 \cong \angle 8$ whether or not $l \parallel m$ since they are vertical angles, which are always congruent.

Lines

Examine the above diagram. If $l \parallel m$ , give in terms of .

$92 - \frac{1}{2}x$

$184 - \frac{1}{2}x$

$47 - \frac{1}{2}x$

Explanation

The two marked angles are same-side interior angles of parallel lines, which are supplementary - that is, their measures have sum 180. We can solve for in this equation:

$2y \div 2 = \left ( 184 -x \right )\div 2$

$y= 92 - \frac{1}{2}x$

Two vertical angles have measures $(3x+14)^{\circ }$ and $\left ( 5x-17\right )^{\circ }$ . Which is the lesser of the measures (or the common measure) of the two angles?

$60\frac{1}{2} ^{\circ }$

$15\frac{1}{2}^{\circ }$

$22\frac{7}{8}^{\circ}$

$68\frac{5}{8}^{\circ}$

$41\frac{1}{8}^{\circ}$

Explanation

Two vertical angles - angles which share a vertex and whose union is a pair of lines - have the same measure. Therefore, we set up and solve the equation