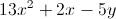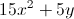Because of our order of operations, the division problem needs to come first. We list the subtraction last because we are subtracting a number by the quotient, so the quotient needs to be listed first.

Remember, order of operations is PEMDAS= parentheses, exponents, multiplication/division, addition/subtraction.

Difference means the answer to a subtraction problem. Because we are adding a number to the difference, we need to do the subtraction problem first. Since we are adding and subtracting in this question, we do not need to use parentheses because with addition and subtraction you work the problem out from left to right. So first we have the subtraction problem, then we add.

Remember, order of operations is PEMDAS= parentheses, exponents, multiplication/division, addition/subtraction.

When you are asked to find the product that means we are going to multiply. Because we are multiplying and dividing in this question, we do not need to use parentheses because with multiplication and division you work the problem out from left to right. So first we have the division problem, then we multiply because it says to find the product of the quotient (answer to a division problem), which means we need to divide first.

Remember, order of operations is PEMDAS= parentheses, exponents, multiplication/division, addition/subtraction.

The phrase "less than the product" means that we are going to subtract from the answer of our multiplication problem. Because of our order of operations, multiplication will come beore subtraction so we do not need to use parentheses.

Remember, order of operations is PEMDAS= parentheses, exponents, multiplication/division, addition/subtraction.

Remember, when there is a subtraction outside of a group, you should add the opposite of each member. That is:

That is a bit confusing, so let's simplify. When you add a negative, you subtract:

Now, group your like variables:

Finally, perform the subtractions and get:

Begin by distributing the through the group:

Next, perform the multiplications:

Group the like terms:

Combine like terms:

Rearrange the terms to get the answer as it appears in the answer choices.

When you are asked to find the product that means we are going to multiply. Because we are multiplying and dividing in this question, we do not need to use parentheses because with multiplication and division you work the problem out from left to right. So first we have the division problem, then we multiply because it says to find the product of the quotient (answer to a division problem), which means we need to divide first.

Remember, order of operations is PEMDAS= parentheses, exponents, multiplication/division, addition/subtraction.

To simplify this expression, combine like terms. In this expression, and are like terms. They are like terms because each term consists of a single variable,, and a numeric coefficient. Add the coefficients of these terms. Addition is the operation that you would use denoted by a plus sign next to the x.

and are also like terms. They are like terms because each term consists of a single variable, , and a numeric coefficient. These two like terms are separated by a subtraction sign, therefore subtraction is the operation you would use

Therefore, the correct answer is

To simplify this expression, combine like terms. In this expression, and are like terms. They are like terms because each term consists of a , and a numeric coefficient. Add the coefficients of these terms. Addition is the operation that you would use denoted by a plus sign.

and are also like terms. They are like terms because each term consists of and a numeric coefficient. These two like terms are separated by a addition sign, therefore addition is the operation you would use.

Therefore, the correct answer is

Combine all the like terms.

The terms can be combined together, which gives you .

When you combine the terms together, you get .

There is only one term so it doesn't get combined with anything. Put them all together and you get

.