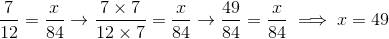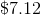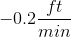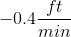HiSet: High School Equivalency Test: Math
Help Questions
HiSET › HiSet: High School Equivalency Test: Math
A quadratic function 
None of the other choices gives the correct response.
Explanation
A polynomial function with zeroes 3 and 7 has as its factors 


Apply the FOIL method to rewrite the polynomial:
Collect like terms:

the correct choice.
What is the vertex of the following quadratic polynomial?
Explanation
Given a quadratic function
the vertex will always be

Thus, since our function is



We plug these variables into the formula to get the vertex as

Hence, the vertex of
is

What is 25% of 
Explanation
Solve for 
by isolating 
First, subtract 17 from both sides:
Now, divide both sides by 2:
One way to find 25% of this value is to multiply 41 by 25 and divide by 100:

the correct choice.
What is the coefficient of the second highest term in the expression: 
Explanation
Step 1: Rearrange the terms from highest power to lowest power.
We will get: 
Step 2: We count the second term from starting from the left since it is the second highest term in the rearranged expression.
Step 3: Isolate the term.
The second term is
Step 4: Find the coefficient. The coefficient of a term is considered as the number before any variables. In this case, the coefficient is 
So, the answer is 
Solve the following equation:
Explanation
The first step to solving an equation where 
Now that the radical is isolated, clear the radical by raising both sides to the power of 3. Note:
Now we want to isolate the 
Finally, divide both sides by 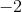

Add or subtract:
Explanation
Step 1: Find the Least Common Denominator of these fraction. We will list out multiples of each denominator until we find a common number for all three fractions...
The smallest common denominator is 
Step 2: Since the denominator is 

Step 3: Add up all the values of x...
Step 4: The result from step 

Final Answer:
Three friends go in on a pizza, which costs $10.49 before 6% tax. Mike agrees to pay $4, and Mickey and Morris agree to split the remainder of the cost evenly. How much will Morris pay?
Explanation
6% of 10.49 is equal to

which, to the nearest cent, rounds to 
Add this tax to the price of the pizza; the amount paid is
Mike pays $4, so Morris will pay half the remainder, or

A swimming pool was drained of water. At 8:56 AM, the water in the pool was 5.7 ft high. At 9:10 AM, the water level in the pool was 2.9 ft high.
Using this information, determine the average rate of change in water height during this period of time.
Explanation
The value we are trying to find is an average rate of decrease. In other words, we are looking for how much, on average, the water level decreased in a minute. To find the average, take the total difference in water level and divide it by the total difference in time.
The total change in water height is given by the ending height minus the starting height:
The total change in time is the amount of minutes that pass between 8:56 AM and 9:10 PM:
Therefore, the average rate of decrease is 
The graph of a function is shown below, with labels on the y-axis hidden.

Determine which of the following functions best fits the graph above.
Explanation
Use the zeroes of the graph to determine the matching function. Zeroes are values of x where 
Visually, you can see that the curve crosses the x-axis when 


A function with a factor of 






The answer choice 



The equation
has two distinct solutions. What is their sum?
Explanation
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 




















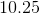




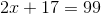

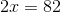







![\sqrt[3]{5-2x}+5=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072122/gif.latex)

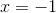
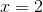

![x=\sqrt[3]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072121/gif.latex)
![\sqrt[3]{5-2x}+5=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072123/gif.latex)
![\sqrt[3]{5-2x}+5-5=4-5](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1082121/gif.latex)
![\sqrt[3]{5-2x}=-1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072124/gif.latex)

![(\sqrt[3]{5-2x})^3=(-1)^3](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1082123/gif.latex)