Physical Chemistry - GRE Subject Test: Chemistry
Card 0 of 196
Which of the following is relevant for real gases, but irrelevant for ideal gases?
I. Volume of gas particles
II. Intermolecular forces between gas particles
III. Volume of container
Which of the following is relevant for real gases, but irrelevant for ideal gases?
I. Volume of gas particles
II. Intermolecular forces between gas particles
III. Volume of container
There are two main assumptions for an ideal gas (and a few smaller assumptions). First, the gas particles of the ideal gas must have no molecular volume. Second, the gas particles must exert no intermolecular forces on each other; therefore, forces such hydrogen bonding, dipole-dipole interactions, and London dispersion forces are irrelevant in ideal gases. Other small assumptions of ideal gases include random particle motion (no currents), lack of intermolecular interaction with the container walls, and completely elastic collisions (a corollary of zero intermolecular forces).
For real gases, however, these assumptions are invalid. This means that the real gas particles have molecular volume and exert intermolecular forces on each other.
Recall that the volume in the ideal gas law is the volume of the free space available inside the container. For ideal gases, the free space volume is equal to the volume of the container because the gas particles take up no volume; however, for real gases, the free space volume is the volume of the container minus the volume of the gas particles. Though the exact values of free space volume will differ, the volume of the container is important for both real and ideal gases.
There are two main assumptions for an ideal gas (and a few smaller assumptions). First, the gas particles of the ideal gas must have no molecular volume. Second, the gas particles must exert no intermolecular forces on each other; therefore, forces such hydrogen bonding, dipole-dipole interactions, and London dispersion forces are irrelevant in ideal gases. Other small assumptions of ideal gases include random particle motion (no currents), lack of intermolecular interaction with the container walls, and completely elastic collisions (a corollary of zero intermolecular forces).
For real gases, however, these assumptions are invalid. This means that the real gas particles have molecular volume and exert intermolecular forces on each other.
Recall that the volume in the ideal gas law is the volume of the free space available inside the container. For ideal gases, the free space volume is equal to the volume of the container because the gas particles take up no volume; however, for real gases, the free space volume is the volume of the container minus the volume of the gas particles. Though the exact values of free space volume will differ, the volume of the container is important for both real and ideal gases.
Compare your answer with the correct one above
Consider a real gas with a constant amount and a constant pressure. It has a temperature of 
and a volume of 
. If you double the temperature, what will happen to the volume?
Consider a real gas with a constant amount and a constant pressure. It has a temperature of
This question can be solved using either Charles's law or the ideal gas law (converted into the combined gas law).
Charles's Law: 
Ideal Gas Law: 
The question states that the pressure and moles 
are held constant; therefore, the volume and temperature are directly proportional. If the question were asking about an ideal gas, the volume would double when you double the temperature
The volume would double for an ideal gas; however, the question is asking about a real gas. To find the correct relationship between volume and temperature we need to look at the equation for real gas volume. Remember that the volume we are concerned with is the volume of the free space in the container, given by the container volume minus the volume of the gas particles. The equation for real gas volume accounts for the volume of the container and the volume of the gas particles. For a real gas, the volume is given as follows:
In this equation, 
is the number of moles of gas particles and 
is the bigness coefficient. This equation implies that the volume of free space for a real gas is always less than the volume for an ideal gas; therefore, doubling the temperature will produce a volume that is less than the predicted volume for an ideal gas. Our answer, then, must be less than double the initial volume.
Note that for an ideal gas the bigness coefficient, 
, would be zero and the volume of free space 
would be equal to the volume of the container 
. This occurs because the volume of the gas particles is negligible for an ideal gas.
This question can be solved using either Charles's law or the ideal gas law (converted into the combined gas law).
Charles's Law:
Ideal Gas Law:
The question states that the pressure and moles
The volume would double for an ideal gas; however, the question is asking about a real gas. To find the correct relationship between volume and temperature we need to look at the equation for real gas volume. Remember that the volume we are concerned with is the volume of the free space in the container, given by the container volume minus the volume of the gas particles. The equation for real gas volume accounts for the volume of the container and the volume of the gas particles. For a real gas, the volume is given as follows:
In this equation,
Note that for an ideal gas the bigness coefficient,
Compare your answer with the correct one above
Which of the following sets of quantum numbers (
) could correspond to a 
orbital?
Which of the following sets of quantum numbers (
Since we're looking at the 
orbital, we know 
. The range of possible values for 
is 0 to 
. Possible values for 
range 
to 
. Therefore, among the answer choices, 
is the only possible combination of quantum numbers corresponding to an 
orbital.
Since we're looking at the
Compare your answer with the correct one above
Which of the following sets of quantum numbers could correspond to a 
orbital?
Which of the following sets of quantum numbers could correspond to a
Since we're looking at the 
orbital, we know . The range of possible values for is 0 to . Possible values for range to . Therefore, among the answer choices,
is the only possible combination of quantum numbers corresponding to a 
orbital.
Since we're looking at the
is the only possible combination of quantum numbers corresponding to a
Compare your answer with the correct one above
For any given chemical reaction, one can draw an energy diagram. Energy diagrams depict the energy levels of the different steps in a reaction, while also indicating the net change in energy and giving clues to relative reaction rate.
Below, a reaction diagram is shown for a reaction that a scientist is studying in a lab. A student began the reaction the evening before, but the scientist is unsure as to the type of the reaction. He cannot find the student’s notes, except for the reaction diagram below.
Upon further review, the scientist realizes that the reaction in question involved formation of a carbocation that quickly reacted again to form stable products. At which point would we most likely find this carbocation in the above diagram?
For any given chemical reaction, one can draw an energy diagram. Energy diagrams depict the energy levels of the different steps in a reaction, while also indicating the net change in energy and giving clues to relative reaction rate.
Below, a reaction diagram is shown for a reaction that a scientist is studying in a lab. A student began the reaction the evening before, but the scientist is unsure as to the type of the reaction. He cannot find the student’s notes, except for the reaction diagram below.
Upon further review, the scientist realizes that the reaction in question involved formation of a carbocation that quickly reacted again to form stable products. At which point would we most likely find this carbocation in the above diagram?
Point 3 is where you would expect to find a relatively stable intermediate. An intermediate is more stable than a transition state, but not as stable as the original reactants and final products. Stability is inversely proportional to energy, thus we are looking for the point that is between the highest and lowest energies in the reaction. By this logic, point 1 is the reactants, 2 and 4 are transition states, 3 is a stable intermediate, and 5 is the products.
Point 3 is where you would expect to find a relatively stable intermediate. An intermediate is more stable than a transition state, but not as stable as the original reactants and final products. Stability is inversely proportional to energy, thus we are looking for the point that is between the highest and lowest energies in the reaction. By this logic, point 1 is the reactants, 2 and 4 are transition states, 3 is a stable intermediate, and 5 is the products.
Compare your answer with the correct one above
What kinetic equation describes the rate of an E1 process?
What kinetic equation describes the rate of an E1 process?
Most organic reactions are carried out in multiple steps. The rate equation can be derived from the process that occurs in the slowest step of the mechanism. An E1 reaction's slow step is when a leaving group separates from the hydrocarbon and a carbocation is formed. The only reactant in this step is one molar equivalent of the hydrocarbon. Thus, the rate equation only depends on that substance. The molar equivalent determines the exponent of each reactant in the equation.
Most organic reactions are carried out in multiple steps. The rate equation can be derived from the process that occurs in the slowest step of the mechanism. An E1 reaction's slow step is when a leaving group separates from the hydrocarbon and a carbocation is formed. The only reactant in this step is one molar equivalent of the hydrocarbon. Thus, the rate equation only depends on that substance. The molar equivalent determines the exponent of each reactant in the equation.
Compare your answer with the correct one above
You want to find the order of each reactant by manipulating the reactant concentrations in multiple trials. The table below shows the effect of altered reactant concentrations on initial reaction rate.
Using the above trials, write the rate law for the reaction.
You want to find the order of each reactant by manipulating the reactant concentrations in multiple trials. The table below shows the effect of altered reactant concentrations on initial reaction rate.
Using the above trials, write the rate law for the reaction.
Keep in mind that the chemical equation and its coefficients have NOTHING to do with the rate law. The order of each reactant must be determined by experiment.
To find the order of each reactant, compare the initial reaction rates of two trials in which only one of the three reactants' concentrations is altered. For example, trials 1 and 4 keep A and B equal, but C is doubled. When C is doubled, we see that the initial reaction rate is quadrupled. As a result, we determine that the order of reactant C is 2. When the reactant is altered, but the initial reaction rate is kept constant, as seen in trials 1 and 3 with respect to A, the order of that reactant is 0. Finally, when the reactant is multiplied by the same factor that the initial reaction rate is multiplied, as seen in trials 1 and 2 with respect to B, the order of the reactant is 1.
Putting the data together: A is zeroth order, B is first order, and C is second order. Our rate law can thus be written 
.
Keep in mind that the chemical equation and its coefficients have NOTHING to do with the rate law. The order of each reactant must be determined by experiment.
To find the order of each reactant, compare the initial reaction rates of two trials in which only one of the three reactants' concentrations is altered. For example, trials 1 and 4 keep A and B equal, but C is doubled. When C is doubled, we see that the initial reaction rate is quadrupled. As a result, we determine that the order of reactant C is 2. When the reactant is altered, but the initial reaction rate is kept constant, as seen in trials 1 and 3 with respect to A, the order of that reactant is 0. Finally, when the reactant is multiplied by the same factor that the initial reaction rate is multiplied, as seen in trials 1 and 2 with respect to B, the order of the reactant is 1.
Putting the data together: A is zeroth order, B is first order, and C is second order. Our rate law can thus be written
Compare your answer with the correct one above
A scientist is studying a reaction, and places the reactants in a beaker at room temperature. The reaction progresses, and she analyzes the products via NMR. Based on the NMR readout, she determines the reaction proceeds as follows:
In an attempt to better understand the reaction process, she varies the concentrations of the reactants and studies how the rate of the reaction changes. The table below shows the reaction concentrations as she makes modifications in three experimental trials.
Reaction rates depend on reaction concentrations, as well as the reaction constant 
. The Arrhenius equation is used to calculate this constant. Which of the following factors is used in the Arrhenius equation?
I. Temperature
II. Activation energy
III. Reactant concentrations
A scientist is studying a reaction, and places the reactants in a beaker at room temperature. The reaction progresses, and she analyzes the products via NMR. Based on the NMR readout, she determines the reaction proceeds as follows:
In an attempt to better understand the reaction process, she varies the concentrations of the reactants and studies how the rate of the reaction changes. The table below shows the reaction concentrations as she makes modifications in three experimental trials.
Reaction rates depend on reaction concentrations, as well as the reaction constant
I. Temperature
II. Activation energy
III. Reactant concentrations
If you thought all of these factors are used in the Arrhenius equation, consider that the rate constant is independent of the reactant concentrations. The concentration effect is considered in the rate law by multiplying the concentrations by the constant, but the concentrations themselves are independent of the actual Arrhenius calculation.
The calculation shows that 
. In this equation, 
is the activation energy and 
is the temperature.
If you thought all of these factors are used in the Arrhenius equation, consider that the rate constant is independent of the reactant concentrations. The concentration effect is considered in the rate law by multiplying the concentrations by the constant, but the concentrations themselves are independent of the actual Arrhenius calculation.
The calculation shows that
Compare your answer with the correct one above
A scientist is studying a reaction, and places the reactants in a beaker at room temperature. The reaction progresses, and she analyzes the products via NMR. Based on the NMR readout, she determines the reaction proceeds as follows:
In an attempt to better understand the reaction process, she varies the concentrations of the reactants and studies how the rate of the reaction changes. The table below shows the reaction concentrations as she makes modifications in three experimental trials.
Which of the following most closely approximates the rate law for this reaction?
A scientist is studying a reaction, and places the reactants in a beaker at room temperature. The reaction progresses, and she analyzes the products via NMR. Based on the NMR readout, she determines the reaction proceeds as follows:
In an attempt to better understand the reaction process, she varies the concentrations of the reactants and studies how the rate of the reaction changes. The table below shows the reaction concentrations as she makes modifications in three experimental trials.
Which of the following most closely approximates the rate law for this reaction?
The reaction table in the passage indicates that the reaction rate varies in a 1-to-1 fashion as you vary the each reactant, while holding the other constant.
The rate law is written as 
.
Compare trials 1 and 2 to see that doubling the ammonium concentration doubles the rate. The reaction is first order for ammonium: 
.
Compare trials 2 and 3 to see that tripling nitrate concentration triples the rate. The reaction is first order for nitrate: 
.
The final rate law is 
.
The reaction table in the passage indicates that the reaction rate varies in a 1-to-1 fashion as you vary the each reactant, while holding the other constant.
The rate law is written as
Compare trials 1 and 2 to see that doubling the ammonium concentration doubles the rate. The reaction is first order for ammonium:
Compare trials 2 and 3 to see that tripling nitrate concentration triples the rate. The reaction is first order for nitrate:
The final rate law is
Compare your answer with the correct one above
For the reaction, 
, the initial rate of the reaction was determined and the values are tabulated below.
What is the overall order for the rate law of this reaction?
For the reaction,
What is the overall order for the rate law of this reaction?
For the reaction given:
We need to find the reaction order, therefore we have to find the values of a and b in the equation. First, let us compare the results of the experiments done to determine how changing the concentration effects the rate of the reaction. Let's compare run number 1 with run number 2 in which the concentration of Y was doubled in run 2 while keeping the concentration of X constant. We can observe that the reaction rate was quadrupled. Let's compare by ratios:
The value for the concentration of B was the same for run 1 and 2 and therefore they cancel out:
Plugging the values into the equation gives:
Simplifying the above equation gives:
Therefore, 
We can also compare the results of run number 2 and run number 3. In that case, the concentration of Y was kept constant while the concentration of X was doubled. We can see that the reaction rate doubled. Therefore the reaction is first order with respect to X and second order with respect to Y. Therefore, the reaction is third order overall:
For the reaction given:
We need to find the reaction order, therefore we have to find the values of a and b in the equation. First, let us compare the results of the experiments done to determine how changing the concentration effects the rate of the reaction. Let's compare run number 1 with run number 2 in which the concentration of Y was doubled in run 2 while keeping the concentration of X constant. We can observe that the reaction rate was quadrupled. Let's compare by ratios:
The value for the concentration of B was the same for run 1 and 2 and therefore they cancel out:
Plugging the values into the equation gives:
Simplifying the above equation gives:
Therefore,
We can also compare the results of run number 2 and run number 3. In that case, the concentration of Y was kept constant while the concentration of X was doubled. We can see that the reaction rate doubled. Therefore the reaction is first order with respect to X and second order with respect to Y. Therefore, the reaction is third order overall:
Compare your answer with the correct one above
For the reaction, 
, the initial rate of the reaction was determined and the values are tabulated below.
Determine the overall order for the rate law of this reaction.
For the reaction,
Determine the overall order for the rate law of this reaction.
For the reaction given:
We need to find the reaction order, therefore we have to find the values of x and y in the equation. First, let us compare the results of the experiments done to determine how changing the concentration effects the rate of the reaction. Let's compare run number 1 with run number 2 in which the concentration of A was doubled in run 2 while keeping the concentration of B constant. We can observe that the reaction rate was doubled. Let's compare by ratios:
The value for the concentration of B was the same for run 1 and 2 and therefore they cancel out:
Plugging the values into the equation gives:
Simplifying the above equation gives:
Therefore, 
We can also compare the results of run number 2 and run number 3. In that case, the concentration of A was kept constant while the concentration of B was decreased by half. We can see that the reaction rate decreased by half. Therefore the reaction is first order with respect to A and first order with respect to B. Therefore, the reaction is second order overall:
For the reaction given:
We need to find the reaction order, therefore we have to find the values of x and y in the equation. First, let us compare the results of the experiments done to determine how changing the concentration effects the rate of the reaction. Let's compare run number 1 with run number 2 in which the concentration of A was doubled in run 2 while keeping the concentration of B constant. We can observe that the reaction rate was doubled. Let's compare by ratios:
The value for the concentration of B was the same for run 1 and 2 and therefore they cancel out:
Plugging the values into the equation gives:
Simplifying the above equation gives:
Therefore,
We can also compare the results of run number 2 and run number 3. In that case, the concentration of A was kept constant while the concentration of B was decreased by half. We can see that the reaction rate decreased by half. Therefore the reaction is first order with respect to A and first order with respect to B. Therefore, the reaction is second order overall:
Compare your answer with the correct one above
Given the enthalpies of formation, what is the enthalpy of combustion of octane in the reaction:
Given the enthalpies of formation, what is the enthalpy of combustion of octane in the reaction:
The equation for enthalpy of reaction is:
Given our chemical reaction and the enthalpies of formation, we can find the enthalpy of reaction.
First, find the total enthalpy for the products.
Then, find the total enthalpy for the reactants.
Since the oxygen is elemental, its heat of formation is zero.
Return to the original equation to calculate the final enthalpy of reaction.
The equation for enthalpy of reaction is:
Given our chemical reaction and the enthalpies of formation, we can find the enthalpy of reaction.
First, find the total enthalpy for the products.
Then, find the total enthalpy for the reactants.
Since the oxygen is elemental, its heat of formation is zero.
Return to the original equation to calculate the final enthalpy of reaction.
Compare your answer with the correct one above
Propane gas combusts according the following chemical equation:
Given the following standard enthalpy values, what is the enthalpy of the reaction for the combustion of one mole of propane?
Propane gas combusts according the following chemical equation:
Given the following standard enthalpy values, what is the enthalpy of the reaction for the combustion of one mole of propane?
Given the molar enthalpy values for reactants and products, we can solve for the enthalpy of the reaction using the equation:
Keep in mind that the molar enthalpy values must be multiplied by the coefficients that are present in the balanced reaction:
Oxygen is omitted because its enthalpy value is zero.
Given the molar enthalpy values for reactants and products, we can solve for the enthalpy of the reaction using the equation:
Keep in mind that the molar enthalpy values must be multiplied by the coefficients that are present in the balanced reaction:
Oxygen is omitted because its enthalpy value is zero.
Compare your answer with the correct one above
Which is not characteristic of an endothermic reaction?
Which is not characteristic of an endothermic reaction?
An endothermic reaction absorbs energy in the form of heat. An endothermic reaction involves breaking of chemical bonds because it involves the absorption of energy. Endothermic reactions tend to feel cold because it is taking heat away from your skin. Since endothermic reactions involve absorbing energy, often in the form of heat, the change in enthalpy is positive.
Therefore, the answer is "releasing of energy to surroundings" which is not a characteristic of an endothermic process. Instead, it is a characteristic of an exothermic reaction which is the direct opposite of an endothermic reaction.
An endothermic reaction absorbs energy in the form of heat. An endothermic reaction involves breaking of chemical bonds because it involves the absorption of energy. Endothermic reactions tend to feel cold because it is taking heat away from your skin. Since endothermic reactions involve absorbing energy, often in the form of heat, the change in enthalpy is positive.
Therefore, the answer is "releasing of energy to surroundings" which is not a characteristic of an endothermic process. Instead, it is a characteristic of an exothermic reaction which is the direct opposite of an endothermic reaction.
Compare your answer with the correct one above
Which of the following reactions has a positive value for change in entropy 
?
Which of the following reactions has a positive value for change in entropy
Entropy is a measure of the disorder of a system. In other words, when the components of a system become more uniform and spread out, the entropy of the system has increased. For example, when a liquid becomes gaseous, the molecules separate from one another, increasing the disorder of the system. As a result, the evaporation of water results in an increase in entropy.
All other options result in a more ordered system, which decreases entropy.
Entropy is a measure of the disorder of a system. In other words, when the components of a system become more uniform and spread out, the entropy of the system has increased. For example, when a liquid becomes gaseous, the molecules separate from one another, increasing the disorder of the system. As a result, the evaporation of water results in an increase in entropy.
All other options result in a more ordered system, which decreases entropy.
Compare your answer with the correct one above
At 
, a reaction has a Gibb's free energy change of 
. If the enthalpy change of the reaction is 
, what is the entropy change of the reaction?
At
We can relate enthalpy, entropy, and Gibb's free energy using the Gibb's free energy equation:
Keep in mind that temperature must be in Kelvin. Since we know enthalpy and Gibb's free energy for the reaction, we can solve for the entropy change:
We can relate enthalpy, entropy, and Gibb's free energy using the Gibb's free energy equation:
Keep in mind that temperature must be in Kelvin. Since we know enthalpy and Gibb's free energy for the reaction, we can solve for the entropy change:
Compare your answer with the correct one above
What was the final temperature of the water if a 
sample of water absorbs 
of heat energy and heats up from 
? (specific heat of water= 
)
What was the final temperature of the water if a
Specific heat is the amount of heat needed to raise 1 gram of a substance by 1oC. Calorimeters used for these types of experiments because they are designed to be well-insulated, so no heat is gained from or lost to the surroundings.
Rearranging gives,
Specific heat is the amount of heat needed to raise 1 gram of a substance by 1oC. Calorimeters used for these types of experiments because they are designed to be well-insulated, so no heat is gained from or lost to the surroundings.
Rearranging gives,
Compare your answer with the correct one above
Which of the following options indicates that a chemical reaction is unfavorable?
Which of the following options indicates that a chemical reaction is unfavorable?
The sign of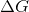 
indicates the direction of a chemical reaction and determines if a reaction is spontaneous or not. A chemical reaction in which 
is considered to be a spontaneous reaction because it will proceed without requiring any outside energy. To approach this problem, we must consider the equation for the Gibbs free energy of a reaction, 
. A reaction is considered to be favorable when 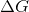is negative. The second law of thermodynamics indicates that the entropy of the universe is spontaneously increasing. This corresponds to a positive 
.
The sign of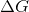
Compare your answer with the correct one above
Use the following values for water as needed.
If burning wood releases 
of heat energy per gram of wood consumed, what mass of wood must be consumed to heat 
of water from 
to 
, and then to convert it to water vapor?
Use the following values for water as needed.
If burning wood releases
There are two processes requiring added heat in this problem:
1. Raising the temperature of the liquid water from 
to 
(use 
)
2. Boiling the water at a constant temperature of 
(use 
)
To use either of these equation, we need to find the mass of the water using the relation between mass, density, and volume.
Use this mass with the given specific heat and temperatures to find the heat for part 1 of the process.
Then, use the mass with the given heat of vaporization to find the energy needed to convert the water to water vapor.
Sum the energies for step 1 and step 2.
This is the total amount of energy needed from the burning wood. Use stoichiometry to find the grams of wood needed to produce this amount of energy.
There are two processes requiring added heat in this problem:
1. Raising the temperature of the liquid water from
2. Boiling the water at a constant temperature of
To use either of these equation, we need to find the mass of the water using the relation between mass, density, and volume.
Use this mass with the given specific heat and temperatures to find the heat for part 1 of the process.
Then, use the mass with the given heat of vaporization to find the energy needed to convert the water to water vapor.
Sum the energies for step 1 and step 2.
This is the total amount of energy needed from the burning wood. Use stoichiometry to find the grams of wood needed to produce this amount of energy.
Compare your answer with the correct one above
Calculate the specific heat of 
of metal that requires 
of heat energy to raise its temperature from 
to 
?
Calculate the specific heat of
Specific heat is the amount of heat needed to raise 1 gram of a substance by 1oC. Calorimeters used for these types of experiments because they are designed to be well-insulated, so no heat is gained from or lost to the surroundings.
Specific heat is the amount of heat needed to raise 1 gram of a substance by 1oC. Calorimeters used for these types of experiments because they are designed to be well-insulated, so no heat is gained from or lost to the surroundings.
Compare your answer with the correct one above