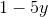GRE Quantitative Reasoning - How to simplify a fraction

For how many integers, , between 26 and 36 is it true that

$\frac{3}{x}_{,}\frac{4}{x}_{,}$ and $\frac{5}{x}$ are all in lowest terms?

Explanation

If is even, then $\frac{4}{x}$ is not in lowest terms, since both and 4 are divisible by 2. Therefore, the only possibilities are 27,29,31,33, and 35. But $\frac{3}{27}= \frac{1}{9}$ , $\frac{3}{33}= \frac{1}{11}$ , and $\frac{5}{35}= \frac{1}{7}$ , so only two integers satisfy the given condition: 29 and 31.

A train travels at a constant rate of meters per second. How many kilometers does it travel in minutes? $(1\ km=1000\ m)$

Explanation

Set up the conversions as fractions and solve:

$\dpi{100} \small \frac{20m}{1sec}\times \frac{60sec^}{1min}\times \frac{1km}{1000m}\times \frac{10min}{1}$

Simplify the fraction:

$\frac{0.0003(0.4)(0.0002)}{0.00000006(0.01)}$

Explanation

To simplify the fraction

$\frac{0.0003(0.4)(0.0002)}{0.00000006(0.01)}$

It may be helpful to write it in terms of scientific notation:

$\frac{3\cdot 10^{-4}(4\cdot 10^{-1})(2\cdot 10^{-4})}{6\cdot 10^{-8}(1\cdot 10^{-2})}$

$\frac{24\cdot 10^{-4-1-4}}{6\cdot 10^{-8-2}}$

$\frac{24\cdot 10^{-9}}{6\cdot 10^{-10}}$

$4\cdot10^{-9+10}$

$4\cdot10$

Mrs. Lawrence's class has students, of which are girls. If you were to choose a student at random, what's the probability that the student chosen would be a boy?

$\frac{3}{5}$

$\frac{2}{5}$

$\frac{2}{7}$

$\frac{2}{5}$

Explanation

In order to find out the probability of choosing a boy, you must first find out how many boys there are. Since there are girls out of students, students should be boys.

Therefore, the probability of choosing a boy is,

$\frac{21}{35}$ .

However, this is not one of the answer choices; therefore, you must reduce the fraction.

In order to reduce a fraction, you have to find their GCM, or greatest common multiple. This is the biggest number that will go into both the numerator and denominator . The largest number is . Divide both the top and bottom by , and you will get the answer:

$\frac{3}{5}$

Simplify:

$\frac{x^{2}y-5x^{2}y^{2}}{x^{2}y}$

$5+x^{2}y^{2}$

None of the other answers

Explanation

With this problem the first thing to do is cancel out variables. The x2 can all be divided by each other because they are present in each system. The equation will now look like this:

$\frac{y-5y^{2}}{y}$

Now we can see that the equation can all be divided by y, leaving the answer to be:

Simplify:

$\frac{x^2-y^2}{x+y}$

$x-y,\ x+y$

Explanation

_x_2 – _y_2 can be also expressed as (x + y)(x – y).

Therefore, the fraction now can be re-written as (x + y)(x – y)/(x + y).

This simplifies to (x – y).

Reduce the fraction:

$\frac{12}{96}$

$\frac{1}{8}$

$\frac{1}{4}$

$\frac{3}{24}$

$\frac{4}{16}$

$\frac{7}{12}$

Explanation

The numerator and denominator are both divisible by 12. Thus, we divide both by 12 to get our final answer.

If we instead divide by another common factor, we may need to complete the process again to make sure that we have completely reduced the fraction.

In mathematical words we get the following:

$\frac{12}{96}=\frac{1 \cdot 12}{8 \cdot 12}=\frac{1}{8}$

Simplify:

$\frac{x\sqrt{2}-2\sqrt{2}}{\sqrt{2x}+2}$

$\sqrt{x}-\sqrt{2}$

$\sqrt{x}+\sqrt{2}$

$x-\sqrt{2}$

$x+\sqrt{2}$

$\frac{x+2}{\sqrt{x-2}}$

Explanation

Notice that the $\sqrt{2}$ term appears frequently. Let's try to factor that out:

$\frac{x\sqrt{2}-2\sqrt{2}}{\sqrt{2x}+2} = \frac{\sqrt{2}*(x-2)}{\sqrt{2}*(\sqrt{x} +\sqrt{2})} = \frac{x-2}{\sqrt{x} +\sqrt{2}}$

Now multiply both the numerator and denominator by the conjugate of the denominator:

$\frac{x-2}{\sqrt{x} +\sqrt{2}} * \frac{\sqrt{x} -\sqrt{2}}{\sqrt{x} -\sqrt{2}} =\frac{(x-2)*(\sqrt{x} -\sqrt{2})}{x-2} =\sqrt{x} -\sqrt{2}$

Which quantity is greater?

Quantity A

$\frac{6}{33}+\frac{17}{24}$

Quantity B

$\frac{17}{32}+\frac{7}{25}$

Quantity A is greater.

Quantity B is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Explanation

This can be solved using 2 methods.

The most time-efficient solution would recognize that $\frac{17}{24}$ is the largest value and nearly equals the sum the other fraction by itself.

The more time consuming method would be to convert each fraction to decimal form and calculate the sum of each quantity.

Quantity A:

Quantity B:

Simplify the given fraction:

$\frac{120}{6000}$

$\frac{1}{5}$

$\frac{2}{25}$

$\frac{1}{100}$

$\frac{1}{50}$

$\frac{1}{20}$

Explanation

120 goes into 6000 evenly 50 times, so we get 1/50 as our simplified fraction.

How to simplify a fraction

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation