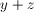GRE Quantitative Reasoning - How to find f(x)

An outpost has the supplies to last 2 people for 14 days. How many days will the supplies last for 7 people?

$\dpi{100} \small 4$

$\dpi{100} \small 7$

$\dpi{100} \small 5$

$\dpi{100} \small 10$

$\dpi{100} \small 9$

Explanation

Supplies are used at the rate of $\dpi{100} \small \frac{Supplies}{Days\times People}$ .

Since the total amount of supplies is the same in either case, $\dpi{100} \small \frac{1}{14\times 2}=\frac{1}{7\times \ (&hash;\ of\ days)}$ .

Solve for days to find that the supplies will last for 4 days.

Find

$f(x)=|x^{2}+4x-127|$

Explanation

Simply plug 6 into the equation and don't forget the absolute value at the end.

absolute value = 67

For which value of are the following two functions equal?

$F(x)=2x+3^x+\frac{9x}{3}$

$G(x)=\frac{2^x+4^x}{2}-4x-5x+1$

Explanation

It is important to follow the order of operations for this equation and find a solution that satisfies both F(x) and G(x).

Recall the order of operations is PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.

The correct answer is 4 because

F(x) = 2_x_ + 3_x_ + (9_x_/3) = 2(4) + 34 + ((9 * 4)/3) = 101, and

G(x) = (((24 + 44)/2) - 4 * 4) – 5(4) + 1 = 101.

If the average of two numbers is $\dpi{100} \small 3y$ and one of the numbers is $\dpi{100} \small y+z$ , what is the other number, in terms of $\dpi{100} \small y$ and $\dpi{100} \small z$ ?

$\dpi{100} \small 5y-z$

$\dpi{100} \small 5y+z$

$\dpi{100} \small y+z$

$\dpi{100} \small 3y+z$

$\dpi{100} \small 4y-z$

Explanation

The average is the sum of the terms divided by the number of terms. Here you have $\dpi{100} \small y+z$ and the other number which you can call $\dpi{100} \small x$ . The average of $\dpi{100} \small x$ and $\dpi{100} \small y+z$ is $\dpi{100} \small 3y$ . So $\dpi{100} \small 3y=\frac{(x+y+z)}{2}$

Multiply both sides by 2.

Solve for $\dpi{100} \small x=5y-z$ .

It takes no more than 40 minutes to run a race, but at least 30 minutes. What equation will model this in m minutes?

$\left | m-35 \right |< 5$

$\left | m+35 \right |< 5$

$\left | m+35 \right |> 5$

$\left | m-35 \right |> 5$

$\left | m-35 \right |= 5$

Explanation

If we take the mean number of minutes to be 35, then we need an equation which is less than 5 from either side of 35. If we subtract 35 from $m$ minutes and take the absolute value, this will give us our equation since we know that the time it takes to run the marathon is between 30 and 40 minutes.

g(x) = 4x – 3

h(x) = .25πx + 5

If f(x)=g(h(x)). What is f(1)?

π + 17

13π + 3

19π – 3

Explanation

First, input the function of h into g. So f(x) = 4(.25πx + 5) – 3, then simplify this expression f(x) = πx + 20 – 3 (leave in terms of πsince our answers are in terms of π). Then plug in 1 for x to get π+ 17.

$11-3x=\frac{5x}{2}$ , solve for .

$x=\frac{1}{2}$

Explanation

The first step is to multiple each side by and that leaves you with

The next step will be to add to both sides resulting in

Finally divide both sides by giving answer of .

What is the value of the function f(x) = 6x2 + 16x – 6 when x = –3?

–108

–12

Explanation

There are two ways to do this problem. The first way just involves plugging in –3 for x and solving 6〖(–3)〗2 + 16(–3) – 6, which equals 54 – 48 – 6 = 0. The second way involves factoring the polynomial to (6x – 2)(x + 3) and then plugging in –3 for x. The second way quickly shows that the answer is 0 due to multiplying by (–3 + 3).

If and , what is ?

Explanation

Plug g(x) into f(x) as if it is just a variable. This gives f(g(x)) = 3(x2 – 12) + 7.

Distribute the 3: 3x2 – 36 + 7 = 3x2 – 29

Worker $\dpi{100} \small A$ can make a trinket in 4 hours, Worker $\dpi{100} \small B$ can make a trinket in 2 hours. When they work together, how long will it take them to make a trinket?

$\dpi{100} \small \ 1 \frac{1}{3}\ hours$

$\dpi{100} \small \frac{1}{2}\ hour$

$\dpi{100} \small 6\ hours$

$\dpi{100} \small 3\ hours$

$\dpi{100} \small \ 1 \frac{1}{2}\ hours$

Explanation

The rates are what needs to be added. Rate $\dpi{100} \small A$ is $\dpi{100} \small \frac{1}{4}$ , or one trinket every 4 hours. Rate $\dpi{100} \small B$ is $\dpi{100} \small \frac{1}{2}$ , one per two hours.