Circles
Help Questions
GRE Quantitative Reasoning › Circles
For 


two
The two values are equal.
Cannot be determined.
Explanation
Therefore the 16 inch pizza is the better deal.
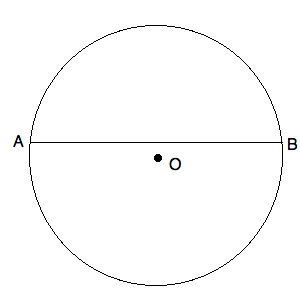
O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Which of the following is true?
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined.
Explanation

O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Do not be tricked by this question. It is true that 







O is the center of the circle above.
The circumference of the circle above is 
Quantity A: The length of 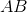
Quantity B:
Which of the following is true?
Quantity B is larger.
Quantity A is larger.
The relationship cannot be determined.
The two quantities are equal.
Explanation
Now, we know that the circumference of a circle is:

This means that the diameter of our circle is must be 



O is the center of the circle above.
The circumference of the circle above is 
Quantity A: The length of 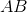
Quantity B:
Which of the following is true?
Quantity B is larger.
Quantity A is larger.
The relationship cannot be determined.
The two quantities are equal.
Explanation
Now, we know that the circumference of a circle is:

This means that the diameter of our circle is must be 



O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Which of the following is true?
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined.
Explanation

O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Do not be tricked by this question. It is true that 






For 


two
The two values are equal.
Cannot be determined.
Explanation
Therefore the 16 inch pizza is the better deal.
For 


two
The two values are equal.
Cannot be determined.
Explanation
Therefore the 16 inch pizza is the better deal.

O is the center of the circle above.
The circumference of the circle above is 
Quantity A: The length of 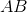
Quantity B:
Which of the following is true?
Quantity B is larger.
Quantity A is larger.
The relationship cannot be determined.
The two quantities are equal.
Explanation
Now, we know that the circumference of a circle is:

This means that the diameter of our circle is must be 



O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Which of the following is true?
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined.
Explanation

O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Do not be tricked by this question. It is true that 






Circle B has a circumference of 36π. What is the area of circle A, which has a radius half the length of the radius of circle B?
9π
324π
81π
18
18π
Explanation
To find the radius of circle B, use the circumference formula (c = πd = 2πr):
2πr = 36π
Divide each side by 2π: r = 18
Now, if circle A has a radius half the length of that of B, A's radius is 18 / 2 = 9.
The area of a circle is πr2. Therefore, for A, it is π*92 = 81π.








