Arithmetic Sequences - GRE Quantitative Reasoning
Card 1 of 88
The first term in a sequence of integers is 2 and the second term is 10. All subsequent terms are the arithmetic mean of all of the preceding terms. What is the 39th term?
The first term in a sequence of integers is 2 and the second term is 10. All subsequent terms are the arithmetic mean of all of the preceding terms. What is the 39th term?
Tap to reveal answer
The first term and second term average out to 6. So the third term is 6. Now add 6 to the preceding two terms and divide by 3 to get the average of the first three terms, which is the value of the 4th term. This, too, is 6 (18/3)—all terms after the 2nd are 6, including the 39th. Thus, the answer is 6.
The first term and second term average out to 6. So the third term is 6. Now add 6 to the preceding two terms and divide by 3 to get the average of the first three terms, which is the value of the 4th term. This, too, is 6 (18/3)—all terms after the 2nd are 6, including the 39th. Thus, the answer is 6.
← Didn't Know|Knew It →
In a sequence of numbers, the first two values are 1 and 2. Each successive integer is calculated by adding the previous two and mutliplying that result by 3. What is fifth value in this sequence?
In a sequence of numbers, the first two values are 1 and 2. Each successive integer is calculated by adding the previous two and mutliplying that result by 3. What is fifth value in this sequence?
Tap to reveal answer
Our sequence begins as 1, 2.
Element 3: (Element 1 + Element 2) * 3 = (1 + 2) * 3 = 3 * 3 = 9
Element 4: (Element 2 + Element 3) * 3 = (2 + 9) * 3 = 11 * 3 = 33
Element 5: (Element 3 + Element 4) * 3 = (9 + 33) * 3 = 42 * 3 = 126
Our sequence begins as 1, 2.
Element 3: (Element 1 + Element 2) * 3 = (1 + 2) * 3 = 3 * 3 = 9
Element 4: (Element 2 + Element 3) * 3 = (2 + 9) * 3 = 11 * 3 = 33
Element 5: (Element 3 + Element 4) * 3 = (9 + 33) * 3 = 42 * 3 = 126
← Didn't Know|Knew It →
Consider the following sequence of integers:
5, 11, 23, 47
What is the 6th element in this sequence?
Consider the following sequence of integers:
5, 11, 23, 47
What is the 6th element in this sequence?
Tap to reveal answer
First, consider the change in each element. Notice that in each case, a given element is twice the preceding one plus one:
11 = 2 * 5 + 1
23 = 11 * 2 + 1
47 = 23 * 2 + 1
To find the 6th element, continue following this:
The 5th: 47 * 2 + 1 = 95
The 6th: 95 * 2 + 1 = 191
First, consider the change in each element. Notice that in each case, a given element is twice the preceding one plus one:
11 = 2 * 5 + 1
23 = 11 * 2 + 1
47 = 23 * 2 + 1
To find the 6th element, continue following this:
The 5th: 47 * 2 + 1 = 95
The 6th: 95 * 2 + 1 = 191
← Didn't Know|Knew It →
The sequence  begins with the numbers
begins with the numbers  and has the
and has the  term defined as
term defined as  , for
, for  .
.
What is the value of the  term of the sequence?
term of the sequence?
The sequence 




What is the value of the 
Tap to reveal answer
The first term of the sequence is  , so here
, so here  , and we're interested in finding the 20th term, so we'll use n = 20.
, and we're interested in finding the 20th term, so we'll use n = 20.
Plugging these values into the given expression for the nth term gives us our answer.

 and
and 

The first term of the sequence is 

Plugging these values into the given expression for the nth term gives us our answer.

← Didn't Know|Knew It →
Let Z represent a sequence of numbers  wherein each term is defined as seven less than three times the preceding term. If
wherein each term is defined as seven less than three times the preceding term. If  , what is the first term in the sequence?
, what is the first term in the sequence?
Let Z represent a sequence of numbers 

Tap to reveal answer
Let us first write the value of a consecutive term in a numerical format:

Consequently,

Using the first equation, we can define  in terms of
in terms of  :
:

This allows us to rewrite

as

Rearrangement of terms allows us to solve for  :
:


Now, using our second equation, we can find  , the first term:
, the first term:

Let us first write the value of a consecutive term in a numerical format:
Consequently,
Using the first equation, we can define 

This allows us to rewrite
as
Rearrangement of terms allows us to solve for 
Now, using our second equation, we can find 
← Didn't Know|Knew It →
What is the sum of the odd integers  ?
?
What is the sum of the odd integers 
Tap to reveal answer
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
← Didn't Know|Knew It →
A sequence is defined by the following formula:


What is the 4th element of this sequence?
A sequence is defined by the following formula:
What is the 4th element of this sequence?
Tap to reveal answer
With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite  as :
as :

You then continue for the third and the fourth element:
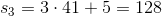

With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite 
You then continue for the third and the fourth element:
← Didn't Know|Knew It →
What is the sum of the 40th and the 70th elements of the series defined as:


What is the sum of the 40th and the 70th elements of the series defined as:
Tap to reveal answer
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between  and
and  . Notice that for every element after the first one, you subtract
. Notice that for every element after the first one, you subtract  . Thus, for the second element you have:
. Thus, for the second element you have:

For the third, you have:

Therefore, for the 40th and 70th elements, you will have:


The sum of these two elements is:
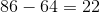
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between 


For the third, you have:
Therefore, for the 40th and 70th elements, you will have:
The sum of these two elements is:
← Didn't Know|Knew It →
The sequence  is defined by:
is defined by:


What is  ?
?
The sequence 
What is 
Tap to reveal answer
Begin by interpreting the general definition:

This means that every number in the sequence is five greater than the element preceding it. For instance:

It is easiest to count upwards:



Begin by interpreting the general definition:
This means that every number in the sequence is five greater than the element preceding it. For instance:
It is easiest to count upwards:
← Didn't Know|Knew It →
The sequence  is defined by:
is defined by:


What is the value of  ?
?
The sequence 
What is the value of 
Tap to reveal answer
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:

This means that for every element in the list, each one is  greater than the one preceding it. For instance:
greater than the one preceding it. For instance:

Now, notice that the first element is:

The second is:

The third could be represented as:

And so forth...
Now, notice that for the third element, there are only two instances of  . We could rewrite our sequence:
. We could rewrite our sequence:

This value will always "lag behind" by one. Therefore, for the  st element, you will have:
st element, you will have:

For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
← Didn't Know|Knew It →
The sequence  is defined by:
is defined by:


What is the value of  ?
?
The sequence 
What is the value of 
Tap to reveal answer
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:

This means that for every element in the list, each one is  less than the one preceding it. For instance:
less than the one preceding it. For instance:
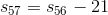
Now, notice that the first element is:
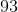
The second is:

The third could be represented as:

And so forth...
Now, notice that for the third element, there are only two instances of  . We could rewrite our sequence:
. We could rewrite our sequence:

This value will always "lag behind" by one. Therefore, for the  th element, you will have:
th element, you will have:

For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
← Didn't Know|Knew It →
What is the sum of the odd integers  ?
?
What is the sum of the odd integers 
Tap to reveal answer
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
← Didn't Know|Knew It →
A sequence is defined by the following formula:


What is the 4th element of this sequence?
A sequence is defined by the following formula:
What is the 4th element of this sequence?
Tap to reveal answer
With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite  as :
as :

You then continue for the third and the fourth element:
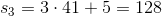

With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite 
You then continue for the third and the fourth element:
← Didn't Know|Knew It →
What is the sum of the 40th and the 70th elements of the series defined as:


What is the sum of the 40th and the 70th elements of the series defined as:
Tap to reveal answer
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between  and
and  . Notice that for every element after the first one, you subtract
. Notice that for every element after the first one, you subtract  . Thus, for the second element you have:
. Thus, for the second element you have:

For the third, you have:

Therefore, for the 40th and 70th elements, you will have:


The sum of these two elements is:
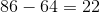
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between 


For the third, you have:
Therefore, for the 40th and 70th elements, you will have:
The sum of these two elements is:
← Didn't Know|Knew It →
The sequence  is defined by:
is defined by:


What is  ?
?
The sequence 
What is 
Tap to reveal answer
Begin by interpreting the general definition:

This means that every number in the sequence is five greater than the element preceding it. For instance:

It is easiest to count upwards:



Begin by interpreting the general definition:
This means that every number in the sequence is five greater than the element preceding it. For instance:
It is easiest to count upwards:
← Didn't Know|Knew It →
The sequence  is defined by:
is defined by:


What is the value of  ?
?
The sequence 
What is the value of 
Tap to reveal answer
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:

This means that for every element in the list, each one is  greater than the one preceding it. For instance:
greater than the one preceding it. For instance:

Now, notice that the first element is:

The second is:

The third could be represented as:

And so forth...
Now, notice that for the third element, there are only two instances of  . We could rewrite our sequence:
. We could rewrite our sequence:

This value will always "lag behind" by one. Therefore, for the  st element, you will have:
st element, you will have:

For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
← Didn't Know|Knew It →
The sequence  is defined by:
is defined by:


What is the value of  ?
?
The sequence 
What is the value of 
Tap to reveal answer
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:

This means that for every element in the list, each one is  less than the one preceding it. For instance:
less than the one preceding it. For instance:
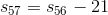
Now, notice that the first element is:
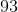
The second is:

The third could be represented as:

And so forth...
Now, notice that for the third element, there are only two instances of  . We could rewrite our sequence:
. We could rewrite our sequence:

This value will always "lag behind" by one. Therefore, for the  th element, you will have:
th element, you will have:

For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
← Didn't Know|Knew It →
What is the sum of the odd integers  ?
?
What is the sum of the odd integers 
Tap to reveal answer
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
Do NOT try to add all of these. It is key that you notice the pattern. Begin by looking at the first and the last elements: 1 and 99. They add up to 100. Now, consider 3 and 97. Just as 1 + 99 = 100, 3 + 97 = 100. This holds true for the entire list. Therefore, it is crucial that we find the number of such pairings.
1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively. Therefore, for each 10s digit, there are 5 pairings, or a total of 500. To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).
Therefore, there are 500 (per pairing) * 5 pairings = 2500.
← Didn't Know|Knew It →
A sequence is defined by the following formula:


What is the 4th element of this sequence?
A sequence is defined by the following formula:
What is the 4th element of this sequence?
Tap to reveal answer
With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite  as :
as :

You then continue for the third and the fourth element:
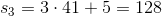

With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite 
You then continue for the third and the fourth element:
← Didn't Know|Knew It →
What is the sum of the 40th and the 70th elements of the series defined as:


What is the sum of the 40th and the 70th elements of the series defined as:
Tap to reveal answer
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between  and
and  . Notice that for every element after the first one, you subtract
. Notice that for every element after the first one, you subtract  . Thus, for the second element you have:
. Thus, for the second element you have:

For the third, you have:

Therefore, for the 40th and 70th elements, you will have:


The sum of these two elements is:
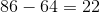
When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between 


For the third, you have:
Therefore, for the 40th and 70th elements, you will have:
The sum of these two elements is:
← Didn't Know|Knew It →