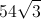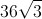Geometry - Hexagons | Practice Hub

In the regular hexagon above, if the length of diagonal is $3\sqrt3$ , what is the area of the hexagon?

Explanation

When all the diagonals of a hexagon are drawn in, you should notice that the long diagonals, marked by solid lines, form congruent equilateral triangles. You should also notice that the other diagonals drawn in with dashed lines are also the heights of two of the equilateral triangles.

Start by using the diagonal to find the length of a side of the hexagon.

Cut the diagonal in half so that we are just left with the height of one equilateral triangle. Notice that the height cleaves the equilateral triangle into two congruent triangles whose sides are in the ratios of $1:\sqrt3:2$ .

Set up a proportion to solve for the length of a side of the triangle.

$\frac{\text{side length}}{2}=\frac{\frac{\text{diagonal}}{2}}{\sqrt3}$

$\text{side length}=\frac{\text{diagonal}}{\sqrt3}$

Plug in the given diagonal to solve for the side length.

$\text{side length}=\frac{3\sqrt3}{\sqrt3}=3$

Now, recall how to find the area of a regular hexagon:

$\text{Area of Hexagon}=\frac{3\sqrt3}{2}(\text{side})^2$

Plug in the side length that you just found in order to find the area.

$\text{Area of Hexagon}=\frac{3\sqrt3}{2}(3)^2=23.38$

Make sure to round to places after the decimal.

Find the perimeter of the regular hexagon.

Explanation

When all the opposite sides of a regular hexagon are connected, you should notice that six congruent equilateral triangles are created:

Thus, the diagonal of the hexagon is twice the length of a side.

$\text{Diagonal}=2(\text{side})$

$\text{Side}=\frac{\text{Diagonal}}{2}$

Plug in the given diagonal to find the length of a side.

$\text{Side}=\frac{14}{2}=7$

Now, recall how to find the perimeter of a regular hexagon:

$\text{Perimeter}=6(\text{side})$

Plug in the side length to find the perimeter.

$\text{Perimeter}=6(7)=42$

An equilateral hexagon has sides of length 6, what is it's area?

$54\sqrt{3}$

$36\sqrt{3}$

$96\sqrt{3}$

Explanation

An equilateral hexagon can be divided into 6 equilateral triangles of side length 6.

The area of a triangle is $0.5\cdot b\cdot h$ . Since equilateral triangles have angles of 60, 60 and 60 the height is $\frac{6\sqrt{3}}{2}$ . This gives each triangle an area of $9\sqrt{3}$ for a total area of the hexagon at $54\sqrt{3}$ or .

Find the perimeter of the regular hexagon.

Explanation

When all the opposite sides of a regular hexagon are connected, you should notice that six congruent equilateral triangles are created:

Thus, the diagonal of the hexagon is twice the length of a side.

$\text{Diagonal}=2(\text{side})$

$\text{Side}=\frac{\text{Diagonal}}{2}$

Plug in the given diagonal to find the length of a side.

$\text{Side}=\frac{14}{2}=7$

Now, recall how to find the perimeter of a regular hexagon:

$\text{Perimeter}=6(\text{side})$

Plug in the side length to find the perimeter.

$\text{Perimeter}=6(7)=42$

A circle is placed inside a regular hexagon as shown in the figure.

If the radius of the circle is $\frac{2}{3}$ , then find the area of the shaded region.

Explanation

In order to find the area of the shaded region, we must first find the areas of the hexagon and the circle.

Recall how to find the area of a regular hexagon.

$\text{Area of Regular Hexagon}=\frac{3\sqrt3}{2}(\text{side})^2$

Substitute in the length of the given side to find the area of the hexagon.

$\text{Area of Regular Hexagon}=\frac{3\sqrt3}{2}(4)^2$

$\text{Area of Regular Hexagon}=24\sqrt3$

Next, recall how to find the area of a circle.

$\text{Area of Circle}=\pi\times\text{radius}^2$

Substitute in the given radius to find the area of the circle.

$\text{Area of Circle}=\pi\times \left(\frac{2}{3}\right)^2$

$\text{Area of Circle}=\frac{4}{9}\pi$

Now, find the area of the shaded region by subtracting the area of the circle from the area of the hexagon.

$\text{Area of Shaded Region}=\text{Area of Hexagon}-\text{Area of Circle}$

$\text{Area of Shaded Region}=24\sqrt3-\frac{4}{9}\pi$

Solve and round to two decimal places.

$\text{Area of Shaded Region}=40.17$

A rectangle is attached to a regular hexagon as shown by the figure.

If the length of the diagonal of the hexagon is , find the area of the entire figure.

Explanation

When all of the diagonals of a regular hexagon are drawn in, you should notice that the hexagon is divided into six congruent equilateral triangles. The length of the diagonal is twice the length of a side of one of the equilateral triangles.

Thus, the diagonal of a hexagon is also twice the length of a side of the regular hexagon.

$\text{Side Length of Hexagon}=\frac{\text{Diagonal of Hexagon}}{2}$

Substitute in the given diagonal to find the side length of the hexagon.

$\text{Side Length of Hexagon}=\frac{14}{2}=7$

Now, recall how to find the area of a regular hexagon.

$\text{Area of Regular Hexagon}=\frac{3\sqrt3(\text{side length})^2}{2}$

Substitute in the value of the side length to find the area of the hexagon.

$\text{Area of Hexagon}=\frac{3\sqrt3(7)^2}{2}=\frac{147\sqrt3}{2}$

Next, notice that the hexagon shares a side with the length of the rectangle.

Recall how to find the area of a rectangle.

$\text{Area of Rectangle}=\text{length}\times\text{width}$

Substitute in the length and the width of the rectangle to find the area.

$\text{Area of Rectangle}=7\times12=84$ .

In order to find the area of the entire figure, add the areas of the hexagon and rectangle together.

$\text{Area of Entire Figure}=\text{Area of Hexagon}+\text{Area of Rectangle}$

$\text{Area of Entire Figure}=\frac{147\sqrt3}{2}+84$

Solve and round to two decimal places.

$\text{Area of Entire Figure}=211.31$

In the regular hexagon above, if the length of diagonal is $3\sqrt3$ , what is the area of the hexagon?

Explanation

Start by using the diagonal to find the length of a side of the hexagon.

Set up a proportion to solve for the length of a side of the triangle.

$\frac{\text{side length}}{2}=\frac{\frac{\text{diagonal}}{2}}{\sqrt3}$

$\text{side length}=\frac{\text{diagonal}}{\sqrt3}$

Plug in the given diagonal to solve for the side length.

$\text{side length}=\frac{3\sqrt3}{\sqrt3}=3$

Now, recall how to find the area of a regular hexagon:

$\text{Area of Hexagon}=\frac{3\sqrt3}{2}(\text{side})^2$

Plug in the side length that you just found in order to find the area.

$\text{Area of Hexagon}=\frac{3\sqrt3}{2}(3)^2=23.38$

Make sure to round to places after the decimal.

If the perimeter of the regular hexagon is , find the length of diagonal .

$2\sqrt3$

$\sqrt3$

The length of the diagonal cannot be determined.

Explanation

When the regular hexagon is divided into congruent equilateral triangles, it's easy to see that diagonal is comprised of two heights of two equilateral triangles. This holds true for the other diagonals when drawn in, as shown by dotted lines in the figure below: