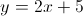Geometry - How to find out if lines are perpendicular

Which line is perpendicular to the given line below?

$y=-\frac{5}{2}x-4$

$y=\frac{2}{5}x$

$y=-\frac{5}{2}x+4$

$y=-\frac{2}{5}x$

$y=\frac{5}{2}x-4$

Explanation

Two perpendicular lines have slopes that are opposite reciprocals, meaning that the sign changes and the reciprocal of the slope is taken.

The original equation is in slope-intercept form,

where represents the slope.

In this case, the slope of the original is:

$m=-\frac{5}{2}$

After taking the opposite reciprocal, the result is the slope below:

$m=\frac{2}{5}$

The slopes of two lines on the coordinate plane are and 4.

True or false: the lines are perpendicular.

True

False

Explanation

Two lines on the coordinate plane are perpendicular if and only if the product of their slopes is . The product of the slopes of the lines in question is

$- 0.25 \cdot 4 = -1$ ,

so the lines are indeed perpendicular.

Two lines intersect at the point . One line passes through the point ; the other passes through .

True or false: The lines are perpendicular.

False

True

Explanation

Two lines are perpendicular if and only if the product of their slopes is . The slope of each line can be found from the coordinates of two points using the slope formula

$m = \frac{y_{2}- y_{1}}{x_{2}-x_{1}}$

To find the slope of the first line, set $x_{1} = 3,y_{1}= 8 , x_{2} = 7, y_{2}= 3$ :

$m = \frac{3-8}{7-3} = \frac{-5}{4} = -\frac{5}{4}$

To find the slope of the second line, set $x_{1} = 3,y_{1}= 8 , x_{2} = -2, y_{2}=1 2$ :

$m = \frac{12-8}{-2-3} = \frac{4}{-5} = -\frac{4}{5}$

The product of the slopes is

$-\frac{5}{4} \left ( -\frac{4}{5} \right )= 1$

As the product is not , the lines are not perpendicular.

Are the lines of the equations

and

parallel, perpendicular, or neither?

Neither

Perpendicular

Parallel

Explanation

Write each equation in the slope-intercept form by solving for ; the -coefficient is the slope of the line.

Subtract from both sides:

The line of this equation has slope .

Subtract from both sides:

Multiply both sides by $\frac{1}{2}$

$\frac{1}{2} \cdot 2y =\frac{1}{2} \cdot ( -x+ 12)$

$y = \frac{1}{2} \cdot( - x)+ \frac{1}{2} \cdot 12$

$y = - \frac{1}{2} x+ 6$

The line of this equation has slope $-\frac{1}{2}$ .

Two lines are parallel if and only if they have the same slope; this is not the case. They are perpendicular if and only if the product of their slopes is ; this is not the case, since

$-2 \times\left ( -\frac{1}{2} \right ) = 1$ .

The correct response is that the lines are neither parallel nor perpendicular.

Are the lines of the equations

and

parallel, perpendicular, or neither?

Neither

Parallel

Perpendicular

Explanation

Write each equation in the slope-intercept form by solving for ; the -coefficient is the slope of the line.

Subtract from both sides:

Multiply both sides by $\frac{1}{2}$ :

$\frac{1}{2} \cdot 2y =\frac{1}{2} \cdot ( - 3x+ 4)$

$y =\frac{1}{2} \cdot ( - 3x) +\frac{1}{2} \cdot 4$

$y =- \frac{3}{2} x + 2$

The slope is the -coefficient $- \frac{3}{2}$

Add to both sides:

Multiply both sides by $\frac{1}{2}$ :

$\frac{1}{2} \cdot 2y = \frac{1}{2} \cdot (3x+ 17)$

$y= \frac{1}{2} \cdot 3x+ \frac{1}{2} \cdot 17$

$y= \frac{3}{2} x+ \frac{17}{2}$

The slope is the -coefficient $\frac{3}{2}$ .

Two lines are parallel if and only if they have the same slope; this is not the case. They are perpendicular if and only if the product of their slopes is ; this is not the case, since $- \frac{3}{2} \times \frac{3}{2} =- \frac{9}{4}$ . The lines are neither parallel nor perpendicular.

Are the lines of the equations

and

parallel, perpendicular, or neither?

Perpendicular

Parallel

Neither

Explanation

Any equation of the form , such as , can be graphed by a vertical line; any equation of the form , such as , can be graphed by a horizontal line. A vertical line and a horizontal line are perpendicular to each other.

Which of the following equations is perpendicular to ?

$y=\frac{1}{3}x +4$

$y=-\frac{1}{3}x+4$

$y=\frac{4}{3}x-1$

$y=-\frac{4}{3}x+5$

Explanation

Convert the given equation to slope-intercept form:

Divide both sides of the equation by :

$y=-x+\frac{4}{3}$

The slope of this function is :

The slope of the perpendicular line will be the negative reciprocal of the original slope. Substitute and solve:

$m_2 = -\frac{1}{m_1}=-\frac{1}{-1}=1$

Only has a slope of .

Given the equation of a line: $y=\frac{3}{5}x+2$

Which equation given below is perpendicular to the given line?

$y=-\frac{5}{3}x+7$

$y=-\frac{3}{5}x-2$

$y=-\frac{3}{2}x-4$

$y=-\frac{3}{5}x+5$

$y=\frac{5}{3}x+2$

Explanation

When looking at the equation of the given line, we know that the slope is $\frac{3}{5}$ and the y-intercept is . Any line perpendicular to the given line will create a 90 degree angle with the given line.

Now, there are INFINITE lines perpendicular to the given line, all with different y-intercepts. So in other words, the line we are looking for will have no dependence on the y-intercept, as any y-intercept will do. What we do care about is the slope of the line.

The slope of any line perpendicular to a given line has a negative reciprocal of the slope. So for this problem:

$given;slope=\frac{3}{5};\rightarrow;perpendicual;slope=-\frac{5}{3}$

The only line that has this slope is

$y=-\frac{5}{3}x+7$

Given the equation of a line:

$y=\frac{1}{2}x+5$

Find the equation of a line parallel to the given line.

$y=\frac{1}{2}x+1$

$y=-\frac{1}{2}x+5$

$y=\frac{1}{2}x+5$

Explanation

Parallel lines will never touch, and therefore they must have the same slope.

Many of the answers are reciprocals or negative slopes, but the slope we are looking for is $\frac{1}{2}$ .

That leaves us with 2 answers. However, one of the answers is the exact same equation for a line as the given equation. Therefore our answer is:

$y=\frac{1}{2}x+1$

The slopes of two lines are 6 and . True or false: the lines are perpendicular.

False

True

Explanation

Two lines on the coordinate plane are perpendicular if and only if the product of their slopes is . The product of the slopes of the lines in question is

$- 0.16666 \cdot 6 = -0.99996$

The product is not equal to , so the lines are not perpendicular.

How to find out if lines are perpendicular

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation