Congruence - Geometry
Card 0 of 956
What is rigid motion?
What is rigid motion?
Rigid motion follows these criteria because the motion is rigid meaning that everything that is moving stays the same except for the location of the entire figure. There are three common types of rigid motion; translation, reflection, and rotation.
Rigid motion follows these criteria because the motion is rigid meaning that everything that is moving stays the same except for the location of the entire figure. There are three common types of rigid motion; translation, reflection, and rotation.
Compare your answer with the correct one above
In terms of rigid motion, how do we know when two figures are congruent to one another?
In terms of rigid motion, how do we know when two figures are congruent to one another?
This is the correct definition in terms of rigid motions. Some of the other options are correct definitions for congruence but do not mention the criteria of there being rigid motion between the two figures. An example of this is that 
and 
are congruent because they are a reflection of one another. Their vertices that map to each other are
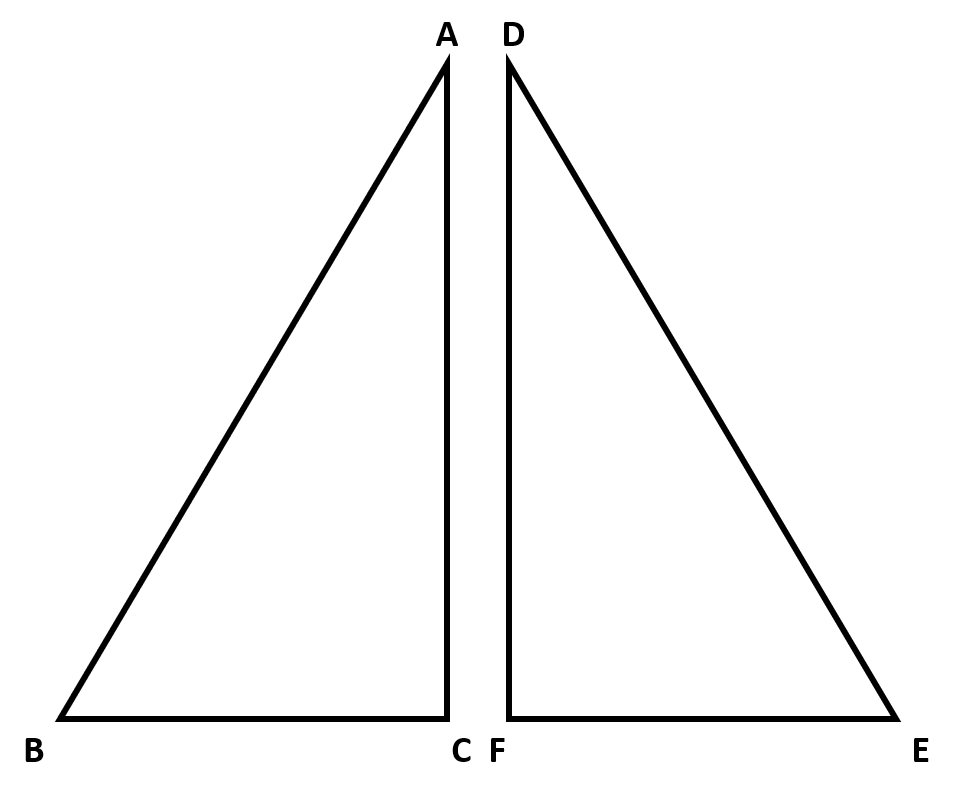
This is the correct definition in terms of rigid motions. Some of the other options are correct definitions for congruence but do not mention the criteria of there being rigid motion between the two figures. An example of this is that 
Compare your answer with the correct one above
True or False: The following triangles are congruent by two different methods:
True or False: The following triangles are congruent by two different methods:
Let’s first begin by showing that these two triangles are congruent through a series of rigid motions. Let’s use our point of reference be 
and 
since we know that these angles are congruent through the information given in the picture. We are able to map 
to 
by reflecting 
along the line 
. So these two triangles are congruent.
Now we will show that these two triangles are congruent through another theorem. We see that there are two pairs of corresponding congruent angles, 
, and the angles’ included sides are congruent as well, 
. The ASA Theorem states that if two triangles share two pairs of corresponding congruent angles and their included sides are congruent, then these two triangles are congruent. So by ASA, these triangles are congruent.
Let’s first begin by showing that these two triangles are congruent through a series of rigid motions. Let’s use our point of reference be 
Now we will show that these two triangles are congruent through another theorem. We see that there are two pairs of corresponding congruent angles, 
Compare your answer with the correct one above
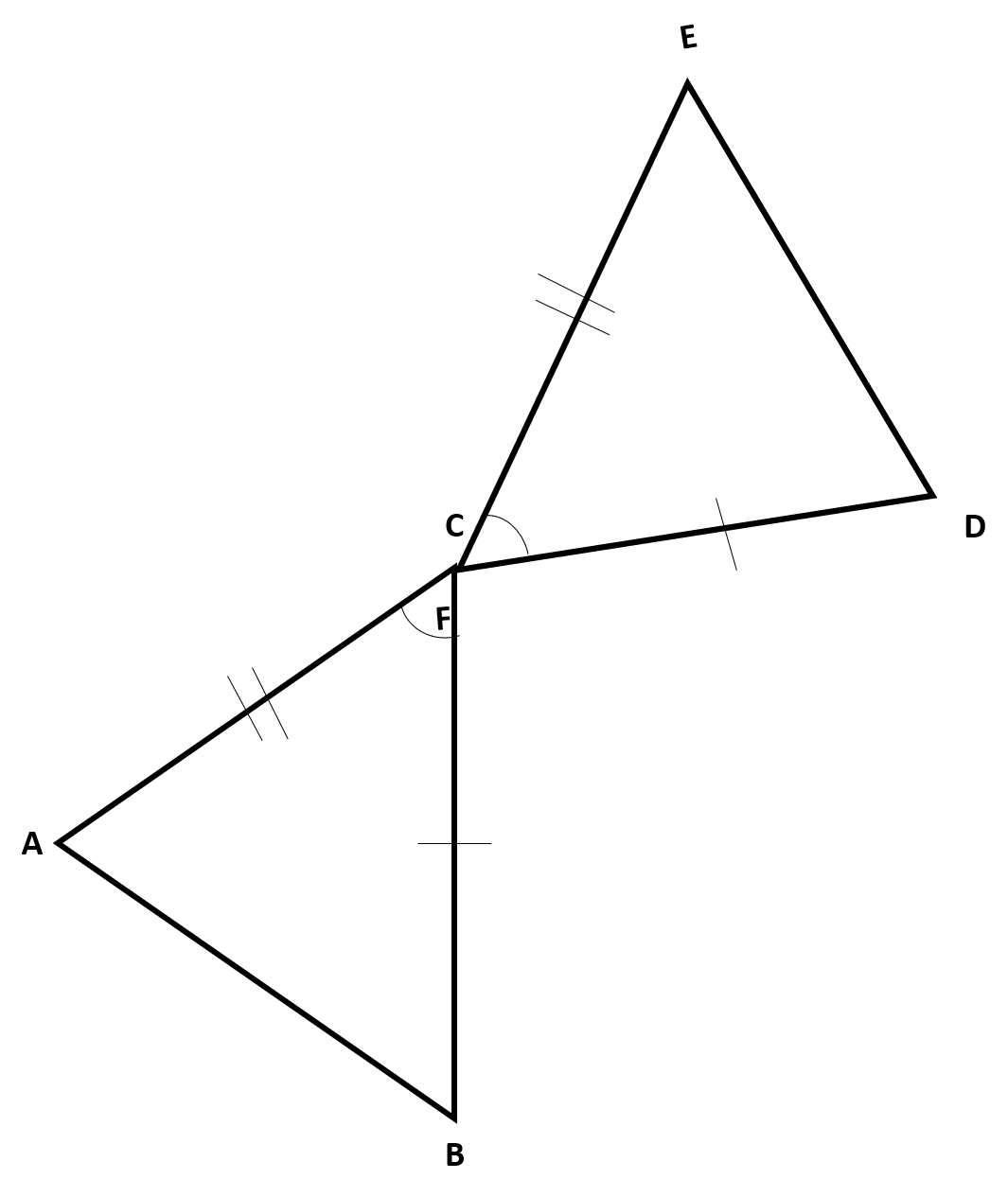
The following two triangles are congruent by the SAS Theorem. What are the series of rigid motions that map them to one another? (Figures not to scale)
The following two triangles are congruent by the SAS Theorem. What are the series of rigid motions that map them to one another? (Figures not to scale)
First, we need to establish a vector that maps at least one pair of vertices. We will use 
to establish a translation between the two figures. This also maps 
to 
.
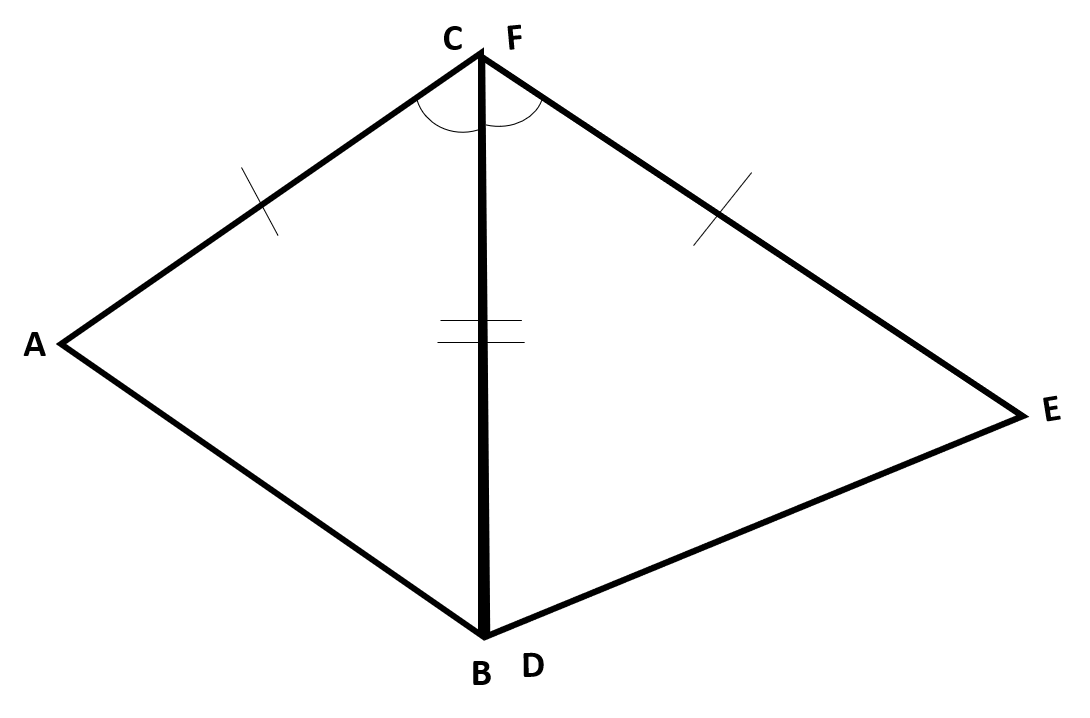
Now they share a vertex and we are able to rotate them together mapping 
to 
and 
to 
.
Now we can reflect across 
mapping 
to 
, 
to 
, and 
to 
.
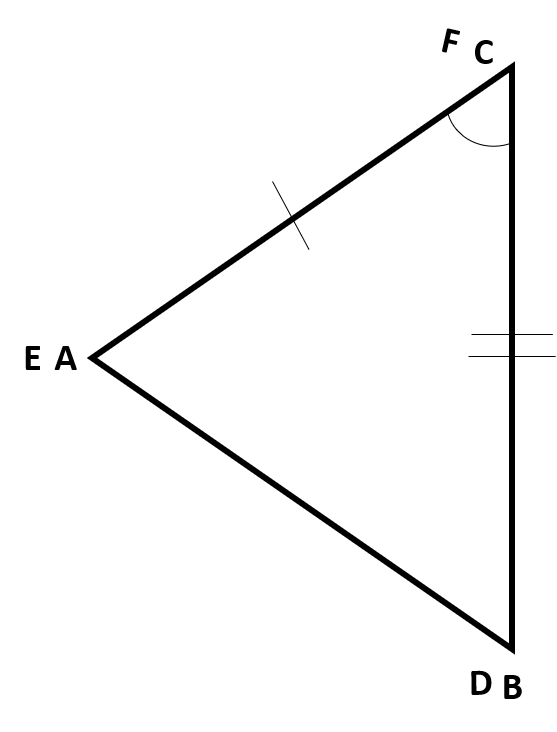
So the order of the series of rigid motions is translation, rotation, reflection.
First, we need to establish a vector that maps at least one pair of vertices. We will use 
Now they share a vertex and we are able to rotate them together mapping 
Now we can reflect across 
So the order of the series of rigid motions is translation, rotation, reflection.
Compare your answer with the correct one above
The following two triangles are congruent by the ASA Theorem. What are the series of rigid motions that map them to one another?
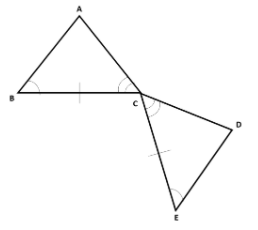
The following two triangles are congruent by the ASA Theorem. What are the series of rigid motions that map them to one another?
First, the two triangles 
and 
share a vertex, so we know that 
maps to 
by the reflective property. Knowing this, we are able to rotate 
to match the congruent sides 
and 
. This maps 
to 
. We can also note that 
maps to 
.
Now we can reflect the triangle 
across 
to map 
to 
, 
to 
and 
to 
.
So the order of rigid motions is rotation, reflection.
First, the two triangles 
Now we can reflect the triangle 
So the order of rigid motions is rotation, reflection.
Compare your answer with the correct one above
Give an informal proof that proves the following two triangles are congruent by the SAS Theorem and by a series of rigid motions.
Give an informal proof that proves the following two triangles are congruent by the SAS Theorem and by a series of rigid motions.
The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 
and so these two triangles are congruent by the SAS theorem. We are able to map 
to 
by rotating 
180 degrees clockwise. So these two triangles are congruent by rigid motion.
The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 
Compare your answer with the correct one above
True or False: If two triangles are congruent through SAS Theorem and share a vertex, they will follow the rigid motions of rotation and reflection.
True or False: If two triangles are congruent through SAS Theorem and share a vertex, they will follow the rigid motions of rotation and reflection.
Consider the triangles 
and 
, where 
. We are able to rotate them together mapping 
to 
and 
to 
.
Now we can reflect across 
mapping 
ro 
, and 
to 
.
Now we are left with the two congruent triangles lying on top of one another, proving that the rigid motions that map these two triangles to one another are rotation and reflection.
Consider the triangles 
Now we can reflect across 
Now we are left with the two congruent triangles lying on top of one another, proving that the rigid motions that map these two triangles to one another are rotation and reflection.
Compare your answer with the correct one above
Triangles that share a side and follow the SSS criteria for congruence follow which of the following rigid motions?
Triangles that share a side and follow the SSS criteria for congruence follow which of the following rigid motions?
Consider the following triangles, 
and 
. They share the side 
. If we reflect triangle 
across 
, we match up all congruent sides, mapping them to one another and mapping 
to 
, 
to 
, and 
to 
, proving these two triangles congruent.
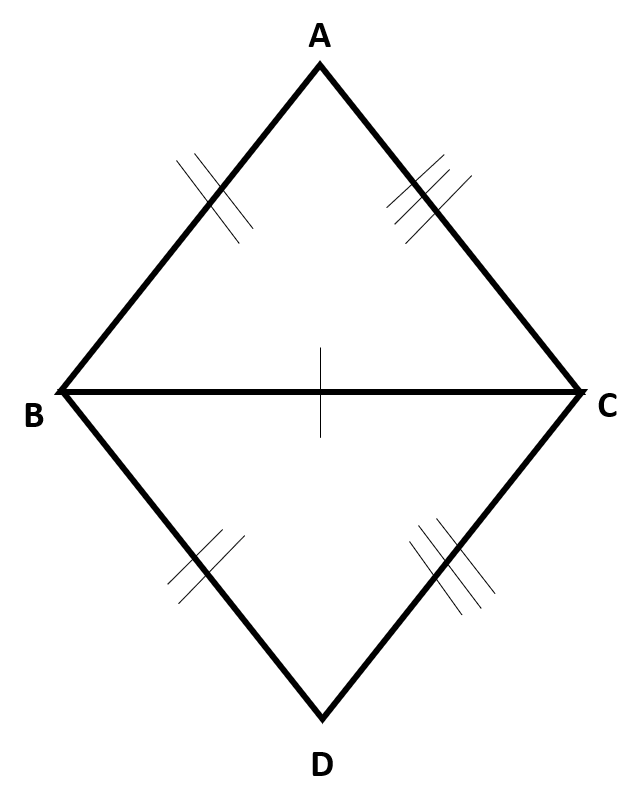
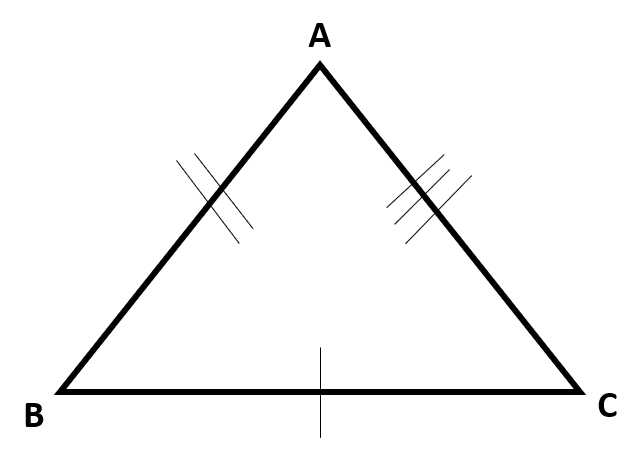
Consider the following triangles, 
Compare your answer with the correct one above
Through which rigid motion are the following triangles related by?
Through which rigid motion are the following triangles related by?
This becomes more clear with the orange line between the two triangles. If flipped over this orange line, the two figures would match up their corresponding congruent parts creating the same triangle.
This becomes more clear with the orange line between the two triangles. If flipped over this orange line, the two figures would match up their corresponding congruent parts creating the same triangle.
Compare your answer with the correct one above
Tell why the following triangles are congruent both by rigid motions and one of the three triangle congruence theorems.
Tell why the following triangles are congruent both by rigid motions and one of the three triangle congruence theorems.
We can see that 
. We know that 
by reflexive property. So by the SSS Theorem, these two triangles are congruent. We can also reflect triangle 
across line 
to map the remaining angles to one another; 
to 
. So these triangles are proven congruent through reflection as well.
We can see that 
Compare your answer with the correct one above
If a triangle is in quadrant three and undergoes a transformation that moves each of its coordinate points to the left three units and down one unit, what transformation has occurred?
If a triangle is in quadrant three and undergoes a transformation that moves each of its coordinate points to the left three units and down one unit, what transformation has occurred?
To determine the type of transformation that is occurring in this particular situation, first recall the different types of transformations.
Translation: To move an object from its original position a certain distance without changing the object in any other way.
Transformation: Refers to any of the four changes that can be done to an object geographically. Transformations include, reflections, translations, rotations, and resizing the object.
Reflection: To flip the orientation of an object over a specific line or function.
Rotation: To rotate an object either clockwise or counter clockwise around a center point.
Since each of the triangle's coordinates is moved to the left and down, it is seen that the size and shape of the triangle remains the same but its location is different. Therefore, the transformation the triangle has undergone is a translation.
To determine the type of transformation that is occurring in this particular situation, first recall the different types of transformations.
Translation: To move an object from its original position a certain distance without changing the object in any other way.
Transformation: Refers to any of the four changes that can be done to an object geographically. Transformations include, reflections, translations, rotations, and resizing the object.
Reflection: To flip the orientation of an object over a specific line or function.
Rotation: To rotate an object either clockwise or counter clockwise around a center point.
Since each of the triangle's coordinates is moved to the left and down, it is seen that the size and shape of the triangle remains the same but its location is different. Therefore, the transformation the triangle has undergone is a translation.
Compare your answer with the correct one above
If a rectangle has the coordinate values, 
, 
, 
, and 
and after a transformation results in the coordinates 
, 
, 
, and 
identify the transformation.
If a rectangle has the coordinate values,
"If a rectangle has the coordinate values, 
, 
, 
, and 
and after a transformation results in the coordinates 
, 
, 
, and 
identify the transformation."
A transformation that changes the 
values by multiplying them by negative one is known as a reflection across the 
-axis or the line 
Therefore, this particular rectangle is being reflected across the 
-axis because the opposite of all the 
values have been taken.
"If a rectangle has the coordinate values,
A transformation that changes the
Therefore, this particular rectangle is being reflected across the
Compare your answer with the correct one above
If a rectangle has the coordinate values, 
, 
, 
, and 
and after a transformation results in the coordinates 
, 
, 
, and 
identify the transformation.
If a rectangle has the coordinate values,
"If a rectangle has the coordinate values, 
, 
, 
, and 
and after a transformation results in the coordinates 
, 
, 
, and 
identify the transformation."
A transformation that changes the 
values by multiplying them by negative one is known as a reflection across the 
-axis or the line 
Therefore, this particular rectangle is being reflected across the 
-axis because the opposite of all the 
values have been taken.
"If a rectangle has the coordinate values,
A transformation that changes the
Therefore, this particular rectangle is being reflected across the
Compare your answer with the correct one above
If a rectangle has the coordinate values, 
, 
, 
, and 
and after a transformation results in the coordinates 
, 
, 
, and 
identify the transformation.
If a rectangle has the coordinate values,
To identify the transformation that is occurring in this particular problem, recall the different transformations.
Translation: To move an object from its original position a certain distance without changing the object in any other way.
Transformation: Refers to any of the four changes that can be done to an object geographically. Transformations include, reflections, translations, rotations, and resizing the object.
Reflection: To flip the orientation of an object over a specific line or function.
Rotation: To rotate an object either clockwise or counter clockwise around a center point.
Looking at the starting and ending coordinates of the rectangle,
, 
, 
, and 
to 
, 
, 
, and 
Since all the 
coordinates are increasing by two this is known as a translation.
To identify the transformation that is occurring in this particular problem, recall the different transformations.
Translation: To move an object from its original position a certain distance without changing the object in any other way.
Transformation: Refers to any of the four changes that can be done to an object geographically. Transformations include, reflections, translations, rotations, and resizing the object.
Reflection: To flip the orientation of an object over a specific line or function.
Rotation: To rotate an object either clockwise or counter clockwise around a center point.
Looking at the starting and ending coordinates of the rectangle,
Since all the
Compare your answer with the correct one above
Assume the values a, b, c, and d are all positive integers. If a rectangle has the coordinate values, (a,b), (c,b), (a,d), and (c,d) and after a transformation results in the coordinates (a,b), (2c,b), (a,2d), and (2c,2d) identify the transformation.
Assume the values a, b, c, and d are all positive integers. If a rectangle has the coordinate values, (a,b), (c,b), (a,d), and (c,d) and after a transformation results in the coordinates (a,b), (2c,b), (a,2d), and (2c,2d) identify the transformation.
The above described transformation is a dilation. Notice that one point, (a,b), stays the same before and after the transformation. The point (c,b) retains the same y value of b, but c is dilated into 2c, extending the base of the rectangle. The point (a,d) is similar in that the x value of a stays the same, but the y value of d is extended or dilated to 2d. The final point (c,d) is extended in both length and width to become (2c,2d). The below graph shows the original figure in blue and the dilated larger figure in pink.
The above described transformation is a dilation. Notice that one point, (a,b), stays the same before and after the transformation. The point (c,b) retains the same y value of b, but c is dilated into 2c, extending the base of the rectangle. The point (a,d) is similar in that the x value of a stays the same, but the y value of d is extended or dilated to 2d. The final point (c,d) is extended in both length and width to become (2c,2d). The below graph shows the original figure in blue and the dilated larger figure in pink.
Compare your answer with the correct one above
Imagine a triangle with vertices located at the points (a,b), (c,d), and (e,f). If this figure were rotated 180o about the origin, what would be the new coordinates of the triangle's vertices?
Imagine a triangle with vertices located at the points (a,b), (c,d), and (e,f). If this figure were rotated 180o about the origin, what would be the new coordinates of the triangle's vertices?
The correct answer is (-a,-b), (-c,-d), and (-e,-f). In other words, you'd just take the opposite value of each x and y value of each vertex of the triangle. The following diagram shows one set of vertexes rotated 180o about the origin to help demonstrate this.
Please note that if one of our original points had any negative values, such as the point (2,-2), and we rotated it 180o about the origin, the signs of both the x and y values would change, and this point's image after translation would be (-2,2).
The correct answer is (-a,-b), (-c,-d), and (-e,-f). In other words, you'd just take the opposite value of each x and y value of each vertex of the triangle. The following diagram shows one set of vertexes rotated 180o about the origin to help demonstrate this.
Please note that if one of our original points had any negative values, such as the point (2,-2), and we rotated it 180o about the origin, the signs of both the x and y values would change, and this point's image after translation would be (-2,2).
Compare your answer with the correct one above
Which of the following describes 
and 
?
Which of the following describes 
To answer this question, we must understand the definition of vertically opposite angles. Vertically opposite angles are angles that are formed opposite of each other when two lines intersect. Vertically opposite angles are always congruent to each other.
To answer this question, we must understand the definition of vertically opposite angles. Vertically opposite angles are angles that are formed opposite of each other when two lines intersect. Vertically opposite angles are always congruent to each other.
Compare your answer with the correct one above
Which of the following describes 
and 
?
Which of the following describes 
To answer this question, we must understand the definition of alternate exterior angles. When a transversal line intersects two parallel lines, 4 exterior angles are formed. Alternate exterior angles are angles on the outsides of these two parallel lines and opposite of each other.
To answer this question, we must understand the definition of alternate exterior angles. When a transversal line intersects two parallel lines, 4 exterior angles are formed. Alternate exterior angles are angles on the outsides of these two parallel lines and opposite of each other.
Compare your answer with the correct one above
True or False: Lines 
and 
are parallel.
True or False: Lines 
We know that lines 
and 
are parallel due to the information we get from the angles formed by the transversal line.
There are:
two pairs of congruent vertically opposite angles
two pairs of congruent alternate interior angles
two pairs of congruent alternate exterior angles
two pairs of congruent corresponding angles
Just using any one of these facts is enough proof that lines 
and 
are parallel.
We know that lines 
There are:
two pairs of congruent vertically opposite angles
two pairs of congruent alternate interior angles
two pairs of congruent alternate exterior angles
two pairs of congruent corresponding angles
Just using any one of these facts is enough proof that lines 
Compare your answer with the correct one above
What does it mean for two angles to be complementary angles?
What does it mean for two angles to be complementary angles?
The definition of complementary angles is: any two angles that sum to 90. We most often see these angles as the two angles in a right triangle that are not the right angle. These two angles do not have to only be in right triangles, however. Complementary triangles are any pair of angles that add up to be 90.
The definition of complementary angles is: any two angles that sum to 90. We most often see these angles as the two angles in a right triangle that are not the right angle. These two angles do not have to only be in right triangles, however. Complementary triangles are any pair of angles that add up to be 90.
Compare your answer with the correct one above