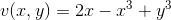Analytic and Harmonic Functions
Help Questions
Complex Analysis › Analytic and Harmonic Functions
Questions 1 - 2
1
Find a Harmonic Conjugate 
Explanation


where 
2
Given 

Nowhere
The Entire Complex Plane
Explanation
Rewriting 
So this implies that
where
Therefore, checking the Cauchy-Riemann Equations, we have that
So the Cauchy-Riemann equations are never satisfied on the entire complex plane, so 
AI TutorYour personal study buddy
Question of the DayDaily practice to build your skills
FlashcardsStudy and memorize key concepts
WorksheetsBuild custom practice quizzes
AI SolverStep-by-step problem solutions
Learn by ConceptMaster concepts step by step
Diagnostic TestsAssess your knowledge level
Practice TestsTest your skills with exam questions
GamesLearn through free games