Polynomial Functions
Help Questions
College Algebra › Polynomial Functions
Find the roots of the function:
Explanation
Factor:
Double check by factoring:
Add together:
Therefore:
Find the roots of the function:
Explanation
Factor:
Double check by factoring:
Add together:
Therefore:
Divide the trinomial below by 
Explanation
We can accomplish this division by re-writing the problem as a fraction.
The denominator will distribute, allowing us to address each element separately.
Now we can cancel common factors to find our answer.
Divide the trinomial below by 
Explanation
We can accomplish this division by re-writing the problem as a fraction.
The denominator will distribute, allowing us to address each element separately.
Now we can cancel common factors to find our answer.
Divide:
Explanation
Divide the leading coefficients to get the first term of the quotient:

Multiply this term by the divisor, and subtract the product from the dividend:
Repeat these steps with the differences until the difference is an integer. As it turns out, we need to repeat only once:


Putting it all together, the quotient can be written as 
Divide:
Explanation
Divide the leading coefficients to get the first term of the quotient:

Multiply this term by the divisor, and subtract the product from the dividend:
Repeat these steps with the differences until the difference is an integer. As it turns out, we need to repeat only once:


Putting it all together, the quotient can be written as 
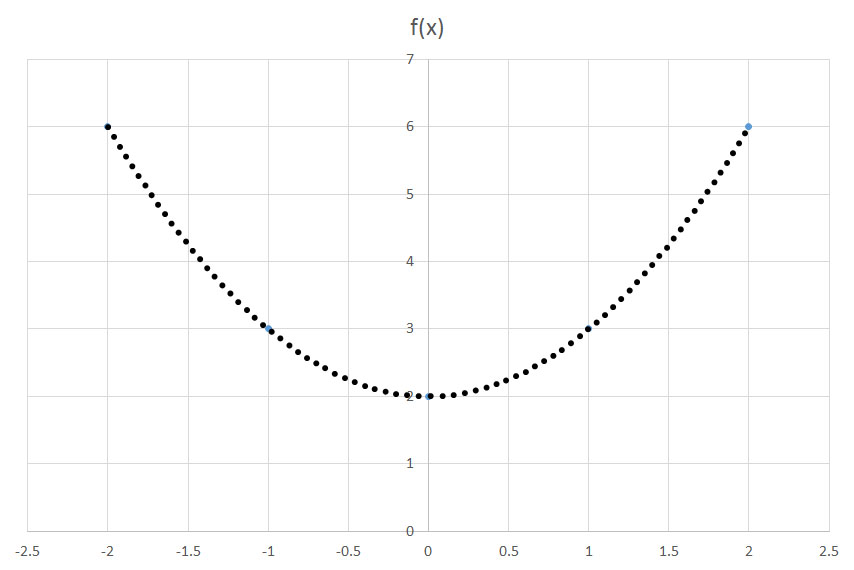
If the function 

Explanation
The function 



To translate along the y-axis, we use the function 


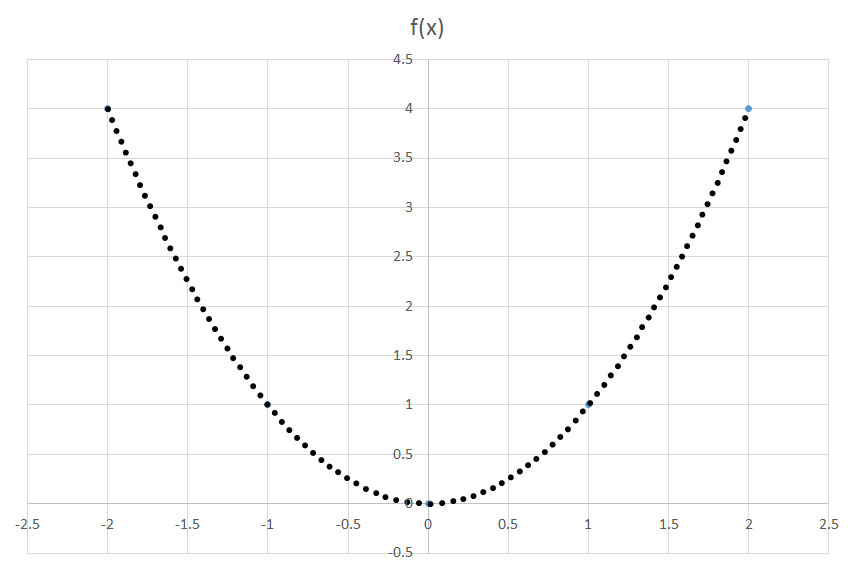
If the function 

Explanation
The function 



To translate along the y-axis, we use the function 

Which of the following graphs matches the function 





Explanation
Start by visualizing the graph associated with the function 

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of 

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function 

Divide:
Explanation
First, rewrite this problem so that the missing 
Divide the leading coefficients:

Multiply this term by the divisor, and subtract the product from the dividend:
Repeat this process with each difference:

One more time:


The quotient is