Calculating Electric Potential
Help Questions
AP Physics C: Electricity and Magnetism › Calculating Electric Potential
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
The potential outside of a charged conducting cylinder with radius 

What is the electric field at a point located at a distance 
Explanation
The radial electric field outside the cylinder can be found using the equation 
Using the formula given in the question, we can expand this equation.
Now, we can take the derivative and simplify.
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Work done by an electric field is given by the product of the charge of the particle, the electric field strength, and the distance travelled.
We are given the charge (



A nonuniformly charged hemispherical shell of radius 

Explanation
Use spherical coordinates with the given surface charge density 






Three equal point charges 

Explanation
Draw a line from the center perpendicular to any side of the triangle. This line divides the side into two equal pieces of length 



A uniformly charged square frame of side length 

You may wish to use the integral:
Explanation
Calculate the potential due to one side of the bar, and then multiply this by 



A uniformly charged hollow spherical shell of radius 



Explanation
Use a spherical coordinate system and place the point of interest a distance 



.
Remarkably, this is the same potential that would exist a distance 

Two point charges 




Explanation
By the Pythagorean theorem, the distance from point P to charge 




A thin bar of length L lies in the xy plane and carries linear charge density 



Explanation
Use the linear charge density 




A nonuniformly charged ring of radius 

Explanation
Use a polar coordinate system, the given linear charge density 
































![=\frac{Rb}{2\epsilon_0} \left[\frac{-\cos^4\theta}{4} \right]_{0}^{\pi/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891699/gif.latex)












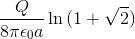



![=\frac{Q}{4\pi\epsilon_{0}a}\left[ \ln\left (\sqrt{x^2+\frac{a^2}{4}} +x\right )\right]_{-a/2}^{a/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891564/gif.latex)









![=\frac{1}{4\pi\epsilon_0} \left (\frac{Q}{2} \right ) \left [\frac{1}{Ra}\sqrt{R^2 + a^2-2Ra\cos\theta} \right ]_{0}^{\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/890844/gif.latex)
















![= \frac{b}{4\pi\epsilon_0}\left [ \sqrt{x^2+a^2}\right ]_{0}^{L}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891578/gif.latex)









![=\frac{b}{4\pi\epsilon_0}\left [\frac{\theta}{2}-\frac{\sin2\theta}{4} \right ]_{0}^{2\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891167/gif.latex)
