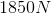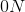AP Physics 2 - Buoyant Force

Seawater density: $1.03\frac{g}{cm^3}$

A baseball has a mass of and a circumference of . Determine what percentage of a baseball will be submerged when it is floating in seawater after a home run?

None of these

Explanation

$F_{net}=F_{gravity}+F_{buoyant}$

$0=\rho_{seawater}*V_{submerged}*g-m*g$

Solving for $V_{submerged}$

$\frac{m_{ball}}{\rho_{seawater}}=V_{submerged}$

Plugging in values

$\frac{145}{1.03}=V_{submerged}$

$V_{submerged}=141cm^3$

If the circumference is , it is

$C=2\pi r=23cm$

$V_{ball}=\frac{4}{3}\pi r^3$

$V_{ball}=\frac{4}{3}\pi *3.66^3$

$V_{ball}=205cm^3$

$\frac{V_{submerged}}{V_{ball}}=\frac{141cm^3}{205cm^3}=69%$

What is the net force on a ball of mass and volume of when it is submerged under water?

$g = 10\frac{m}{s^2}$

$\rho_{water} = 1.0\frac{g}{ml}$

Explanation

The buoyant force on the ball is simply the weight of water displaced by the ball:

$F_b = V_{ball}\cdot\rho_{water}\cdot g = (0.2m^3)(1000\frac{kg}{m^3})(10\frac{m}{s^2}) = 2000 N$

The force of gravity on the ball is:

$F_g = mg = 15kg (10\frac{m}{s^2})= 150 N$

These forces oppose each other, so we can say:

$F_{net} = F_b - F_g = 2000N - 150N = 1850N$

A balloon of mass $45\textup{ g}$ is inflated to a volume of $2\textup{ L}$ with pure . Determine the buoyant force it will experience when submerged in water.

$19.6\textup{ N}$

None of these

$15\textup{ N}$

$28.1\textup{ N}$

$3.4\textup{ N}$

Explanation

Use the equation for buoyant force:

$F_b=\rho*|g|*V$

Where

$\rho$ is the density of the medium

is the acceleration due to gravity

is the volume

Plugging in values:

$F_b=\frac{1kg}{L}*|-9.8\frac{m}{s^2}|*2L$

A semi-hollow, spherical ball with an empty volume of is submerged in water and has an initial mass of . The ball develops a leak and water begins entering the ball at a rate of $0.6\frac{L}{min}$ . How long does it take before the buoyant force on the ball is equal to the gravitational force?

$g = 10\frac{m}{s^2}$

$\rho_w = 1000\frac{kg}{m^3}$

Explanation

We are asked when:

$m_bg = m_{w,displaced}g$

$m_b = m_{w,displaced}$

$m_b = \rho_wV_b$

Now we need to develop an expression for the mass in the ball using the rate at which water enters the ball:

$m_b = m_i + \dot{m}t$

Where:

$\dot{m} = \dot{V}\rho_wt$

$m_b = m_i + \dot{V}\rho_wt$

Plugging this into expression (1):

$m_i + \dot{V}\rho_wt= \rho_wV_b$

Rearranging for time, we get:

$t= \frac{\left ( \rho_wV_b- m_i \right )}{\dot{V}\rho_w}$

Plugging in our values, we get:

$t= \frac{\left ( 1\frac{kg}{L}\right )(0.8L)- (0.4kg)}{\left ( 0.6\frac{L}{min}\right )\left ( 1\frac{kg}{L}\right )}$

$t = \frac{2}{3}min = 40s$

A block of mass is sinking in water at a constant velocity. There is a constant drag force of acting on the block. What is the volume of the block?

$g = 10\frac{m}{s^2}$

$\rho_w = 1000\frac{kg}{m^3}$

Explanation

We will start with Newton's 2nd law for this problem:

$F_{net}=ma$

Since the block is traveling at a constant velocity we can say:

$F_{net}=0$

There are 3 forces acting on the block: gravitational, buoyant, and drag force. If we denote a downward force being positive, the expression becomes:

Where:

$F_g = m_{block}g$

$F_b = m_{w,displaced}g$

Substituting these in:

$m_{block}g - m_{w,displaced}g - 3N = 0$

Where according to Archimedes's principle:

$m_w = \rho_wV_b$

Plugging this in:

$m_{block}g - \rho_w V_bg - 3N = 0$

Rearranging for volume:

$m_{block}g - 3N = \rho_w V_bg$

$V_b = \frac{m_{block}g - 3N }{\rho_w g}$

Plugging in values:

$V_b =\left (\frac{(2kg)\left ( 10\frac{m}{s^2}\right )-3N}{\left ( 1000\frac{kg}{m^3}\right )\left ( 10\frac{m}{s^2}\right )} \right )\left ( \frac{1000L}{1m^3}\right )$

A block with a volume of sinks to the bottom of a water tank. What is the buoyant force on the block?

There is no buoyant force on the block

Explanation

The correct answer is because although the block has sunk, there is still a buoyant force. This buoyant force is the result of the block displacing a volume of water, equal to the block's volume. The weight of the water volume displaced is because was displaced. The weight of is which is equal to the buoyant force on the block.

Determine the net force on a copper ball $\left(\rho_{copper}=8.96\frac{kg}{L}\right)$ of radius submerged into water.

${\rho_{water}=1.0\frac{kg}{L}}$

$5.12*10^{-5}N$

None of these

$6.14*10^{-5}N$

$4.88*10^{-6}N$

$2.11*10^{-3}N$

Explanation

Convert to and calculate volume:

$\frac{4}{3}\pi r^3=V_{sphere}$

$\frac{4}{3}\pi (.005)^3=V_{sphere}$

$5.24*10^{-7}m^3=V_{sphere}$

Calculate buoyant force:

$F_{buoyant}=g*\rho_{medium}*V_{object}$

Plug in values:

$F_{buoyant}=9.8*1*5.24*10^{-7}$

$F_{buoyant}=5.14*10^{-6}N$

Calculate force due to gravity:

$F_g=\rho_{object}*V_{object}*g$

Plug in values and solve:

$F_{gravity}=4.6*10^{-5}N$

$F_{net}=F_1+F_2+...$

Plug in values:

$5.14*10^{-6}+4.6*10^{-5}=F_{net}$

$F_{net}=5.12*10^{-5}N$

Hanging from a scale is a sphere that is totally submerged in a pool of water. If the reading on the scale is , calculate the radius of the sphere.

Explanation

The weight of the object is . If the scale reads , this tells us that the buoyancy force has a magnitude of . Mathematically:

We may relate these parameters by Archimedes' principle:

$\rho_{water} g V_{disp}=10N$

This allows us to solve for the volume of the sphere, and thus, the radius of the sphere.

$\frac{10N}{\rho_{water}g}=V_{disp}=V_{sphere}=\frac{10N}{1000\frac{kg}{m^3}\left(9.81\frac{m}{s^2} \right )}=0.001m^3$

Now we may use the formula for volume of a sphere to solve for the radius:

$V_{sphere}=\frac{4}{3}\pi r^3$

$r=\left(\frac{3}{4\pi}0.001m^3 \right )^{\frac{1}{3}}=0.0624m=6.24cm$

Which of the following statements best describes the buoyant force on an object submerged in water?

The buoyant force is equal to the weight of the water displaced by the object.

The buoyant force is equal to the weight of the object submerged in water.

The buoyant force is equal to the volume of water displaced by the object.

The buoyant force is equal to the weight of all of the water.

None of these accurately describe buoyant force.

Explanation

The correct answer is that the buoyant force is equal to the weight of the water displaced by the object.

It is an upward force that is exerted on the object because of the volume of fluid displaced by that object.

A scuba diver with a total mass is dressed so his density $\rho = 1,000 \frac{kg}{m^3}$ and is holding a spherical ball with a volume while submerged in water. What is the density of the ball if the upward acceleration of the ball and diver is $a = 1.5\frac{m}{s^2}$ ?

$g = 10\frac{m}{s^2}$

$\rho_w = 1000\frac{kg}{m^3}$

$817\frac{kg}{m^3}$

$623\frac{kg}{m^3}$

$424\frac{kg}{m^3}$

$281\frac{kg}{m^3}$

$974\frac{kg}{m^3}$

Explanation

We will start with Newton's 2nd law for this problem:

$F_{net} = ma$

Where there are 4 total forces acting on the scuba diver and ball: gravity and buoyancy acting on both the scuba diver and the ball. However, the diver has the same density as the water, so the gravitational and buoyancy forces acting on the diver will cancel out. If we designate an upward force as being positive, we can say:

$F_{b_{ball}}-F_{g_{ball}}=m_Ta$ (1)

Where:

$F_{b_{ball}}=m_{w,displaced}g$

$F_{g_{ball}}=m_bg$

Where:

$m_w = \rho_w V_b$

$m_b = \rho_b V_b$

So,

$F_b = \rho_w V_bg$

$F_{g}=\rho_bV_bg$

$m_T = m_d+\rho_bV_b$

Plugging these expressions back in to expression (1), we get:

$\rho_w V_bg-\rho_b V_bg = (m_d + \rho_b V_b)a$

Now let's start rearranging for the density of the ball:

$\rho_wV_bg - m_da = \rho_bV_b(a+g)$

$\rho_b = \frac{\rho_wV_bg-m_da}{V_b(a+g)}$

$\rho_b = \frac{\left ( 1000\frac{kg}{m^3}\right )(0.2m^3)\left ( 10\frac{m}{s^2}\right )-(80kg)\left ( 1.5\frac{m}{s^2}\right )}{(0.2m^s)(1.5\frac{m}{s^2}+10\frac{m}{s^2})}$

$\rho_b = 817\frac{kg}{m^3}$

Buoyant Force

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation