Application of Integrals - AP Calculus BC
Card 1 of 220
The temperature of an oven is increasing at a rate  degrees Fahrenheit per miniute for
degrees Fahrenheit per miniute for  minutes. The initial temperature of the oven is
minutes. The initial temperature of the oven is  degrees Fahrenheit.
degrees Fahrenheit.
What is the temperture of the oven at  ? Round your answer to the nearest tenth.
? Round your answer to the nearest tenth.
The temperature of an oven is increasing at a rate 


What is the temperture of the oven at 
Tap to reveal answer
Integrating  over an interval
over an interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/403013/gif.latex) will tell us the total accumulation, or change, in temperature over that interval. Therefore, we will need to evaluate the integral
will tell us the total accumulation, or change, in temperature over that interval. Therefore, we will need to evaluate the integral

to find the change in temperature that occurs during the first five minutes.
A substitution is useful in this case. Let . We should also express the limits of integration in terms of
. We should also express the limits of integration in terms of  . When
. When  , and when
, and when  Making these substitutions leads to the integral
Making these substitutions leads to the integral
 .
.
To evaluate this, you must know the antiderivative of an exponential function.
In general,
 .
.
Therefore,
 .
.
This tells us that the temperature rose by approximately  degrees during the first five minutes. The last step is to add the initial temperature, which tells us that the temperature at
degrees during the first five minutes. The last step is to add the initial temperature, which tells us that the temperature at  minutes is
minutes is
 degrees.
degrees.
Integrating 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/403013/gif.latex)
to find the change in temperature that occurs during the first five minutes.
A substitution is useful in this case. Let




To evaluate this, you must know the antiderivative of an exponential function.
In general,

Therefore,

This tells us that the temperature rose by approximately 


← Didn't Know|Knew It →
Find the equation for the velocity of a particle if the acceleration of the particle is given by:

and the velocity at time  of the particle is
of the particle is  .
.
Find the equation for the velocity of a particle if the acceleration of the particle is given by:
and the velocity at time 

Tap to reveal answer
In order to find the velocity function, we must integrate the accleration function:

We used the rule

to integrate.
Now, we use the initial condition for the velocity function to solve for C. We were told that

so we plug in zero into the velocity function and solve for C:

C is therefore 30.
Finally, we write out the velocity function, with the integer replacing C:

In order to find the velocity function, we must integrate the accleration function:
We used the rule
to integrate.
Now, we use the initial condition for the velocity function to solve for C. We were told that
so we plug in zero into the velocity function and solve for C:
C is therefore 30.
Finally, we write out the velocity function, with the integer replacing C:
← Didn't Know|Knew It →
Find the work done by gravity exerting an acceleration of  for a
for a  block down
block down  from its original position with no initial velocity.
from its original position with no initial velocity.
Remember that

 , where
, where  is a force measured in
is a force measured in  ,
,  is work measured in
is work measured in  , and
, and  and
and  are initial and final positions respectively.
are initial and final positions respectively.
Find the work done by gravity exerting an acceleration of 


Remember that







Tap to reveal answer
The force of gravity is proportional to the mass of the object and acceleration of the object.

Since the block fell down 5 meters, its final position is  and initial position is
and initial position is  .
.

The force of gravity is proportional to the mass of the object and acceleration of the object.
Since the block fell down 5 meters, its final position is 

← Didn't Know|Knew It →
Evaluate the following integral and find the specific function which satisfies the given initial conditions:


Evaluate the following integral and find the specific function which satisfies the given initial conditions:
Tap to reveal answer
Evaluate the following integral and find the specific function which satisfies the given initial conditions:


To solve this problem,we need to evaluate the given integral, then solve for our constant of integration.
Let's begin by recalling the following integration rules:


Using these two, we can integrate f(x)


SO, we get:

We are almost there, but we need to find c. To do so, plug in our initial conditions and solve:



So, our answer is:

Evaluate the following integral and find the specific function which satisfies the given initial conditions:
To solve this problem,we need to evaluate the given integral, then solve for our constant of integration.
Let's begin by recalling the following integration rules:
Using these two, we can integrate f(x)
SO, we get:
We are almost there, but we need to find c. To do so, plug in our initial conditions and solve:
So, our answer is:
← Didn't Know|Knew It →
Determine the volume of a solid created by rotating the curve ![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389789/gif.latex) and the line
and the line  by revolving around the
by revolving around the  -axis.
-axis.
Determine the volume of a solid created by rotating the curve ![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389789/gif.latex)


Tap to reveal answer
Write the volume formula for cylindrical shells.

The shell radius is  .
.
The shell height is the function in terms of  . Rewrite that equation.
. Rewrite that equation.
![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389794/gif.latex)


The bounds lie on the y-axis since the thickness variable is  . This is from 0 to 1, since the intersection of the line
. This is from 0 to 1, since the intersection of the line  and
and ![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389799/gif.latex) is at
is at  .
.
Substitute all the values and solve for the volume.

![V=2\pi \int_${0}^{1}$$(y-y^4$)dy= 2\pi $\left[$\frac{y^2$$}{2}$-$\frac{y^5$}{5}\right]_${0}^{1}$= 2\pi\left[$\frac{1}{2}$-$\frac{1}{5}\right]= $\frac{3}{5}$\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/392849/gif.latex)
Write the volume formula for cylindrical shells.
The shell radius is 
The shell height is the function in terms of 
The bounds lie on the y-axis since the thickness variable is 

![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389799/gif.latex)

Substitute all the values and solve for the volume.
← Didn't Know|Knew It →
Determine the volume of the solid obtained by rotating the region with the following bounds about the x-axis:




Determine the volume of the solid obtained by rotating the region with the following bounds about the x-axis:
Tap to reveal answer
From calculus, we know the volume of an irregular solid can be determined by evaluating the following integral:

Where A(x) is an equation for the cross-sectional area of the solid at any point x. We know our bounds for the integral are x=1 and x=4, as given in the problem, so now all we need is to find the expression A(x) for the area of our solid.
From the given bounds, we know our unrotated region is bounded by the x-axis (y=0) at the bottom, and by the line $y=x^2$-4x+5 at the top. Because we are rotating about the x-axis, we know that the radius of our solid at any point x is just the distance $y=x^2$-4x+5. Now that we have a function that describes the radius of the solid at any point x, we can plug the function into the formula for the area of a circle to give us an expression for the cross-sectional area of our solid at any point:

We now have our equation for the cross-sectional area of the solid, which we can integrate from x=1 to x=4 to find its volume:

![=\pi $[$\frac{1}{5}$x^5$$-2x^4$$+\frac{26}{3}$x^3$$-20x^2$+25x]_${1}^{4}$=\frac{78\pi }{5}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265347/gif.latex)
From calculus, we know the volume of an irregular solid can be determined by evaluating the following integral:
Where A(x) is an equation for the cross-sectional area of the solid at any point x. We know our bounds for the integral are x=1 and x=4, as given in the problem, so now all we need is to find the expression A(x) for the area of our solid.
From the given bounds, we know our unrotated region is bounded by the x-axis (y=0) at the bottom, and by the line $y=x^2$-4x+5 at the top. Because we are rotating about the x-axis, we know that the radius of our solid at any point x is just the distance $y=x^2$-4x+5. Now that we have a function that describes the radius of the solid at any point x, we can plug the function into the formula for the area of a circle to give us an expression for the cross-sectional area of our solid at any point:
We now have our equation for the cross-sectional area of the solid, which we can integrate from x=1 to x=4 to find its volume:
← Didn't Know|Knew It →
Find the volume of the solid generated by revolving the region bounded by  and the
and the  -axis in the first quadrant about the
-axis in the first quadrant about the  -axis.
-axis.
Find the volume of the solid generated by revolving the region bounded by 


Tap to reveal answer
Since we are revolving a region of interest around a horizontal line  , we need to express the inner and outer radii in terms of x.
, we need to express the inner and outer radii in terms of x.
Recall the formula:
![Volume = \pi \int_${b}^{a}$ [(\textup{outer $radius})^{2}$ - (\textup{inner $radius})^{2}$]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343034/gif.latex)
The outer radius is  and the inner radius is
and the inner radius is  . The x-limits of the region are between
. The x-limits of the region are between  and
and  . So the volume set-up is:
. So the volume set-up is:

Using trigonometric identities, we know that:

Hence:

![= \pi \left[$\frac{1}{2}$x - $\frac{1}{4}$sin2x\right]_${0}^{\pi}$ = $$\frac{1}{2}$\pi^2$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343042/gif.latex)
Since we are revolving a region of interest around a horizontal line 
Recall the formula:
The outer radius is 



Using trigonometric identities, we know that:
Hence:
← Didn't Know|Knew It →
Suppose the functions  ,
,  , and
, and  form a closed region. Rotate this region across the x-axis. What is the volume?
form a closed region. Rotate this region across the x-axis. What is the volume?
Suppose the functions 


Tap to reveal answer
Write the formula for cylindrical shells, where  is the shell radius and
is the shell radius and  is the shell height.
is the shell height.

Determine the shell radius.

Determine the shell height. This is done by subtracting the right curve,  , with the left curve,
, with the left curve,  .
.

Find the intersection of  and
and  to determine the y-bounds of the integral.
to determine the y-bounds of the integral.


The bounds will be from 0 to 2. Substitute all the givens into the formula and evaluate the integral.


![V=2\pi \left[ $2y^2$ - $$\frac{1}{4}$y^4$\right]_${0}^{2}$ = 2\pi $\left[2(2)^2$ $-$\frac{1}{4}$(2)^4$\right] = 2\pi[8-4]= 8\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/288906/gif.latex)
Write the formula for cylindrical shells, where 

Determine the shell radius.
Determine the shell height. This is done by subtracting the right curve, 

Find the intersection of 

The bounds will be from 0 to 2. Substitute all the givens into the formula and evaluate the integral.
← Didn't Know|Knew It →
A man fills up a cup of water by leaving it outside during a rainstorm. The rate at which the height of the cup changes is equal to  . What is the height of water at
. What is the height of water at  ? Assume the cup is empty at
? Assume the cup is empty at  .
.
A man fills up a cup of water by leaving it outside during a rainstorm. The rate at which the height of the cup changes is equal to 


Tap to reveal answer
The rate at which the height changes is  , which means
, which means  .
.
To find the height after nine seconds, we need to integrate to get  .
.
We can multiply both sides by  to get
to get  and then integrate both sides.
and then integrate both sides.
This gives us
 .
.
Since the cup is empty at  , so
, so  .
.
This means  . No units were given in the problem, so leaving the answer unitless is acceptable.
. No units were given in the problem, so leaving the answer unitless is acceptable.
The rate at which the height changes is 

To find the height after nine seconds, we need to integrate to get 
We can multiply both sides by 

This gives us

Since the cup is empty at 

This means 
← Didn't Know|Knew It →
Approximate the volume of a solid in the first quadrant revolved about the y-axis and bounded by the functions:  and
and  . Round the volume to the nearest integer.
. Round the volume to the nearest integer.
Approximate the volume of a solid in the first quadrant revolved about the y-axis and bounded by the functions: 

Tap to reveal answer
Write the washer's method.
![V=\int_${a}^{b}$$\pi[R(y)^2$$-r(y)^2$]:dy](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/390110/gif.latex)
Set the equations equal to each other to determine the bounds.



The bounds are from 0 to 3.
Determine the big and small radius. Rewrite the equations so that they are in terms of y.
![R(y)= \sqrt[3]{y}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/390114/gif.latex)

Set up the integral and solve for the volume.
![V=\int_${0}^{3}$$\pi[(\sqrt[3]{y})^2$$-($\frac{y}{9}$)^2$]:dy](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/390116/gif.latex)
![V=\int_${0}^{3}$$\pi[y^{$\frac{2}$${3}$}-$\frac{y^2$}{81}$]:dy=\pi[$\frac{3}{5}$y^$$\frac{5}{3}$-$\frac{y^3$}{243}$]_${0}^{3}$=11.41353](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/390117/gif.latex)
The volume to the nearest integer is: 
Write the washer's method.
Set the equations equal to each other to determine the bounds.
The bounds are from 0 to 3.
Determine the big and small radius. Rewrite the equations so that they are in terms of y.
Set up the integral and solve for the volume.
The volume to the nearest integer is:
← Didn't Know|Knew It →
Find the volume of the solid generated when the function

is revolved around the x-axis on the interval ![[0,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/399976/gif.latex) .
.
Hint: Use the method of cylindrical disks.
Find the volume of the solid generated when the function
is revolved around the x-axis on the interval ![[0,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/399976/gif.latex)
Hint: Use the method of cylindrical disks.
Tap to reveal answer
The formula for the volume is given as

where  and the bounds on the integral come from the interval
and the bounds on the integral come from the interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/405073/gif.latex) .
.
As such,

When taking the integral, we will use the inverse power rule which states

Applying this rule we get

And by the corollary of the First Fundamental Theorem of Calculus
![\pi $\left($\frac{x^3$}{3}\right) \left.\begin{matrix} \ \end{matrix}\right|_${0}^{8}$=\pi $\left(\left[$\frac{8^3$$}{3}\right]-\left[$\frac{0^3$}{3}\right]\right)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/439966/gif.latex)

As such,
 units cubed
units cubed
The formula for the volume is given as
where 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/405073/gif.latex)
As such,
When taking the integral, we will use the inverse power rule which states
Applying this rule we get
And by the corollary of the First Fundamental Theorem of Calculus
As such,

← Didn't Know|Knew It →
What is the volume of the solid formed when the line  is rotated around the
is rotated around the  -axis from
-axis from  to
to  ?
?
What is the volume of the solid formed when the line 



Tap to reveal answer
To rotate a curve around the y-axis, first convert the function so that y is the independent variable by solving  for x. This leads to the function
for x. This leads to the function  .
.
We'll also need to convert the endpoints of the interval to y-values. Note that when  , and when
, and when  Therefore, the the interval being rotated is from
Therefore, the the interval being rotated is from  .
.
The disk method is best in this case. The general formula for the disk method is
 , where V is volume,
, where V is volume,  are the endpoints of the interval, and
are the endpoints of the interval, and  the function being rotated.
the function being rotated.
Substuting the function and endpoints from the problem at hand leads to the integral
 .
.
To evaluate this integral, you must know the power rule. Recall that the power rule is
 .
.
![\pi\int_${2}^{3}$$y^4dy$$=\pi[$\frac{y^5$}{5}$]_${2}^{3}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/402108/gif.latex)

 .
.
To rotate a curve around the y-axis, first convert the function so that y is the independent variable by solving 

We'll also need to convert the endpoints of the interval to y-values. Note that when 


The disk method is best in this case. The general formula for the disk method is



Substuting the function and endpoints from the problem at hand leads to the integral

To evaluate this integral, you must know the power rule. Recall that the power rule is


← Didn't Know|Knew It →
Using the method of cylindrical disks, find the volume of the region revolved around the x-axis of the graph of

on the interval
![[0,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/523909/gif.latex)
Using the method of cylindrical disks, find the volume of the region revolved around the x-axis of the graph of
on the interval
Tap to reveal answer
The formula for volume of the region revolved around the x-axis is given as

where 
As such

When taking the integral, we use the inverse power rule which states

Applying this rule term by term we get

And by the corollary of the Fundamental Theorem of Calculus
![\pi\left( $$\frac{x^5$}{5}$ - $$\frac{20x^4$}{4}$ + $$\frac{94x^3$}{3}$ + $$\frac{60x^2$}{2}$ + 9x\right|_${0}^{10}$=\pi \left( \left[ $$\frac{(10)^5$$}{5}$-$\frac{20(10)^4$$}{4}$+\frac{94(10)^3$$}{3}$+\frac{60(10)^2$}{2}$+9(10) \right]-0 \right)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/523914/gif.latex)

As such the volume is
 units cubed
units cubed
The formula for volume of the region revolved around the x-axis is given as
where
As such
When taking the integral, we use the inverse power rule which states
Applying this rule term by term we get
And by the corollary of the Fundamental Theorem of Calculus
As such the volume is

← Didn't Know|Knew It →
Find the volume of the solid generated by rotating about the y-axis the region under the curve  , from
, from  to
to  .
.
Find the volume of the solid generated by rotating about the y-axis the region under the curve 


Tap to reveal answer
Since we are revolving a function of  around the y-axis, we will use the method of cylindrical shells to find the volume.
around the y-axis, we will use the method of cylindrical shells to find the volume.
Using the formula for cylindrical shells, we have


![=[2\pi $x^{5/2}$$]^${4}$_{0}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/604752/gif.latex)
 .
.
Since we are revolving a function of 
Using the formula for cylindrical shells, we have

← Didn't Know|Knew It →
Find the area bound by the curve of g(t), the x and y axes, and the line 

Find the area bound by the curve of g(t), the x and y axes, and the line
Tap to reveal answer
Find the area bound by the curve of g(t), the x and y axes, and the line 

We are asked to find the area under a curve. This sounds like a job for an integral.
We need to integrate our function from 0 to  . These will be our limits of integration. With that in mind, our integral look like this.
. These will be our limits of integration. With that in mind, our integral look like this.

Now, we need to recall the rules for integrating sine and cosine.


With these rules in mind, we can integrate our original function to get:


Now, we just need to evaluate our new function at the given limits. Let's start with 0

And our upper limit...



Now, we need to take the difference between our limits:

So, our answer is 2.59
Find the area bound by the curve of g(t), the x and y axes, and the line
We are asked to find the area under a curve. This sounds like a job for an integral.
We need to integrate our function from 0 to 
Now, we need to recall the rules for integrating sine and cosine.
With these rules in mind, we can integrate our original function to get:
Now, we just need to evaluate our new function at the given limits. Let's start with 0
And our upper limit...
Now, we need to take the difference between our limits:
So, our answer is 2.59
← Didn't Know|Knew It →
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
Tap to reveal answer
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
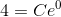

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
← Didn't Know|Knew It →
Determine the volume of a solid created by rotating the curve ![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389789/gif.latex) and the line
and the line  by revolving around the
by revolving around the  -axis.
-axis.
Determine the volume of a solid created by rotating the curve ![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389789/gif.latex)


Tap to reveal answer
Write the volume formula for cylindrical shells.

The shell radius is  .
.
The shell height is the function in terms of  . Rewrite that equation.
. Rewrite that equation.
![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389794/gif.latex)


The bounds lie on the y-axis since the thickness variable is  . This is from 0 to 1, since the intersection of the line
. This is from 0 to 1, since the intersection of the line  and
and ![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389799/gif.latex) is at
is at  .
.
Substitute all the values and solve for the volume.

![V=2\pi \int_${0}^{1}$$(y-y^4$)dy= 2\pi $\left[$\frac{y^2$$}{2}$-$\frac{y^5$}{5}\right]_${0}^{1}$= 2\pi\left[$\frac{1}{2}$-$\frac{1}{5}\right]= $\frac{3}{5}$\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/392849/gif.latex)
Write the volume formula for cylindrical shells.
The shell radius is 
The shell height is the function in terms of 
The bounds lie on the y-axis since the thickness variable is 

![y=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/389799/gif.latex)

Substitute all the values and solve for the volume.
← Didn't Know|Knew It →
Determine the volume of the solid obtained by rotating the region with the following bounds about the x-axis:




Determine the volume of the solid obtained by rotating the region with the following bounds about the x-axis:
Tap to reveal answer
From calculus, we know the volume of an irregular solid can be determined by evaluating the following integral:

Where A(x) is an equation for the cross-sectional area of the solid at any point x. We know our bounds for the integral are x=1 and x=4, as given in the problem, so now all we need is to find the expression A(x) for the area of our solid.
From the given bounds, we know our unrotated region is bounded by the x-axis (y=0) at the bottom, and by the line $y=x^2$-4x+5 at the top. Because we are rotating about the x-axis, we know that the radius of our solid at any point x is just the distance $y=x^2$-4x+5. Now that we have a function that describes the radius of the solid at any point x, we can plug the function into the formula for the area of a circle to give us an expression for the cross-sectional area of our solid at any point:

We now have our equation for the cross-sectional area of the solid, which we can integrate from x=1 to x=4 to find its volume:

![=\pi $[$\frac{1}{5}$x^5$$-2x^4$$+\frac{26}{3}$x^3$$-20x^2$+25x]_${1}^{4}$=\frac{78\pi }{5}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265347/gif.latex)
From calculus, we know the volume of an irregular solid can be determined by evaluating the following integral:
Where A(x) is an equation for the cross-sectional area of the solid at any point x. We know our bounds for the integral are x=1 and x=4, as given in the problem, so now all we need is to find the expression A(x) for the area of our solid.
From the given bounds, we know our unrotated region is bounded by the x-axis (y=0) at the bottom, and by the line $y=x^2$-4x+5 at the top. Because we are rotating about the x-axis, we know that the radius of our solid at any point x is just the distance $y=x^2$-4x+5. Now that we have a function that describes the radius of the solid at any point x, we can plug the function into the formula for the area of a circle to give us an expression for the cross-sectional area of our solid at any point:
We now have our equation for the cross-sectional area of the solid, which we can integrate from x=1 to x=4 to find its volume:
← Didn't Know|Knew It →
Find the volume of the solid generated by revolving the region bounded by  and the
and the  -axis in the first quadrant about the
-axis in the first quadrant about the  -axis.
-axis.
Find the volume of the solid generated by revolving the region bounded by 


Tap to reveal answer
Since we are revolving a region of interest around a horizontal line  , we need to express the inner and outer radii in terms of x.
, we need to express the inner and outer radii in terms of x.
Recall the formula:
![Volume = \pi \int_${b}^{a}$ [(\textup{outer $radius})^{2}$ - (\textup{inner $radius})^{2}$]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343034/gif.latex)
The outer radius is  and the inner radius is
and the inner radius is  . The x-limits of the region are between
. The x-limits of the region are between  and
and  . So the volume set-up is:
. So the volume set-up is:

Using trigonometric identities, we know that:

Hence:

![= \pi \left[$\frac{1}{2}$x - $\frac{1}{4}$sin2x\right]_${0}^{\pi}$ = $$\frac{1}{2}$\pi^2$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343042/gif.latex)
Since we are revolving a region of interest around a horizontal line 
Recall the formula:
The outer radius is 



Using trigonometric identities, we know that:
Hence:
← Didn't Know|Knew It →
Suppose the functions  ,
,  , and
, and  form a closed region. Rotate this region across the x-axis. What is the volume?
form a closed region. Rotate this region across the x-axis. What is the volume?
Suppose the functions 


Tap to reveal answer
Write the formula for cylindrical shells, where  is the shell radius and
is the shell radius and  is the shell height.
is the shell height.

Determine the shell radius.

Determine the shell height. This is done by subtracting the right curve,  , with the left curve,
, with the left curve,  .
.

Find the intersection of  and
and  to determine the y-bounds of the integral.
to determine the y-bounds of the integral.


The bounds will be from 0 to 2. Substitute all the givens into the formula and evaluate the integral.


![V=2\pi \left[ $2y^2$ - $$\frac{1}{4}$y^4$\right]_${0}^{2}$ = 2\pi $\left[2(2)^2$ $-$\frac{1}{4}$(2)^4$\right] = 2\pi[8-4]= 8\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/288906/gif.latex)
Write the formula for cylindrical shells, where 

Determine the shell radius.
Determine the shell height. This is done by subtracting the right curve, 

Find the intersection of 

The bounds will be from 0 to 2. Substitute all the givens into the formula and evaluate the integral.
← Didn't Know|Knew It →