Techniques of antidifferentiation - AP Calculus AB
Card 0 of 1166
A projectile is shot up from a platform  above the ground with a velocity of
above the ground with a velocity of  . Assume that the only force acting on the projectile is gravity that produces a downward acceleration of
. Assume that the only force acting on the projectile is gravity that produces a downward acceleration of  . Find the velocity as a function of
. Find the velocity as a function of  .
.
A projectile is shot up from a platform 



$a=\frac{d^2s$$}{dt^2$}$=\frac{dv}{dt}$=-9.8 with initial conditions v(0)=150
Separate velocity variables and solve.
v=-9.8t+C
Plug in intial conditions
v=-9.8t+150
$a=\frac{d^2s$$}{dt^2$}$=\frac{dv}{dt}$=-9.8 with initial conditions v(0)=150
Separate velocity variables and solve.
v=-9.8t+C
Plug in intial conditions
v=-9.8t+150
Compare your answer with the correct one above
A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of $s=220t-16t^2$ after  seconds. What is its velocity 500 ft into the air?
seconds. What is its velocity 500 ft into the air?
A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of $s=220t-16t^2$ after 
The bullet will be at a height of 500 ft on the way up and on the way down.
We use the position equation  to solve for how long it will take to reach a height = 500.
to solve for how long it will take to reach a height = 500.  and
and  seconds.
seconds.
We then plug that into the velocity equation, which is the derivative of the position function.  .
.
We can see that plugging in the value of  yields
yields  and
and  yields
yields  . The positive and negative values of velocity indicates the up and down direction of travel.
. The positive and negative values of velocity indicates the up and down direction of travel.
The bullet will be at a height of 500 ft on the way up and on the way down.
We use the position equation 


We then plug that into the velocity equation, which is the derivative of the position function. 
We can see that plugging in the value of 



Compare your answer with the correct one above
The position of a particle as a function of time is given below:

At what values of  does the particle change direction?
does the particle change direction?
The position of a particle as a function of time is given below:
At what values of 
In order to find the point at which the particle changes direction, we must determine whenever the velocity of the particle changes sign (from positive to negative, or from negative to positive).
We will need to have the function of the particle's velocity before we can determine where the velocity changes sign. Because the velocity is the derivative of position with respect to time, we can write the function for velocity,  , as follows:
, as follows:


If we set  , then we can determine the points where it can change sign.
, then we can determine the points where it can change sign.



The possible points where  will change signs occur at
will change signs occur at  . However, we need to check to make sure.
. However, we need to check to make sure.
First, we can try a value less than 2, such as 1, and then a value between 2 and 4, such as 3. We will evaluate  at
at  and
and  and see if the sign of the velocity changes.
and see if the sign of the velocity changes.


Thus,  is indeed a point where the velocity changes sign (from positive to negative). This means that the particle does in fact change direction at
is indeed a point where the velocity changes sign (from positive to negative). This means that the particle does in fact change direction at  .
.
Lastly, we will evaluate the velocity at a value of  larger than 4, such as 5.
larger than 4, such as 5.

The sign of the velocity has switched back to positive, so the particle does indeed change direction at  .
.
The answer is  and
and  .
.
In order to find the point at which the particle changes direction, we must determine whenever the velocity of the particle changes sign (from positive to negative, or from negative to positive).
We will need to have the function of the particle's velocity before we can determine where the velocity changes sign. Because the velocity is the derivative of position with respect to time, we can write the function for velocity, 
If we set 
The possible points where 

First, we can try a value less than 2, such as 1, and then a value between 2 and 4, such as 3. We will evaluate 


Thus, 

Lastly, we will evaluate the velocity at a value of 
The sign of the velocity has switched back to positive, so the particle does indeed change direction at 
The answer is 

Compare your answer with the correct one above
A jogger leaves City  at
at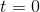 . His subsequent position, in feet, is given by the function:
. His subsequent position, in feet, is given by the function:
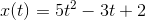 ,
,
where  is the time in minutes.
is the time in minutes.
Find the velocity of the jogger at 15 minutes.
A jogger leaves City 
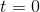
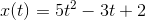
where 
Find the velocity of the jogger at 15 minutes.
To find velocity, one has to use the first derivative of  :
:
 .
.

Note the units have to be ft/min.
To find velocity, one has to use the first derivative of 

Note the units have to be ft/min.
Compare your answer with the correct one above
The speed of a car traveling on the highway is given by the following function of time:

Note that

What does this mean?
The speed of a car traveling on the highway is given by the following function of time:
Note that
What does this mean?
The function  gives you the car's speed at time
gives you the car's speed at time  . Therefore, the fact that
. Therefore, the fact that  means that the car's speed is
means that the car's speed is  at time
at time  . This is equivalent to saying that the car is not moving at time
. This is equivalent to saying that the car is not moving at time  . We have to take the derivative of
. We have to take the derivative of  to make claims about the acceleration.
to make claims about the acceleration.
The function 






Compare your answer with the correct one above
Use a change of variable (aka a u-substitution) to evaluate the integral,

Use a change of variable (aka a u-substitution) to evaluate the integral,

Integrals such as this are seen very commonly in introductory calculus courses. It is often useful to look for patterns such as the fact that the polynomial under the radical in our example,  , happens to be one order higher than the factor outside the radical,
, happens to be one order higher than the factor outside the radical,  You know that if you take a derivative of a second order polynomial you will get a first order polynomial, so let's define the variable:
You know that if you take a derivative of a second order polynomial you will get a first order polynomial, so let's define the variable:
 (1)
(1)
Now differentiate with respect to  to write the differential for
to write the differential for  ,
,
 (2)
(2)
Looking at equation (2), we can solve for  , to obtain
, to obtain  . Now if we look at the original integral we can rewrite in terms of
. Now if we look at the original integral we can rewrite in terms of 

Now proceed with the integration with respect to  .
.

![= $$\frac{1}{2}$\left[$\frac{1}{\frac{1}${2}+1}u^{$\frac{1}${2}$+1} \right ]+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741662/gif.latex)



Now write the result in terms of  using equation (1), we conclude,
using equation (1), we conclude,

Integrals such as this are seen very commonly in introductory calculus courses. It is often useful to look for patterns such as the fact that the polynomial under the radical in our example, 


Now differentiate with respect to 


Looking at equation (2), we can solve for 

Now proceed with the integration with respect to 
Now write the result in terms of 
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable u to substitute for a variable of x.
For this problem, we will let u replace the expression  .
.
Next, we must take the derivative of u. Its derivative is  .
.
Next, solve this equation for dx so that we may replace it in the integral.
Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify.
into the original integral and simplify.
The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral, leaving behind a
in the integral, leaving behind a  . We can pull the
. We can pull the  out front of the integral. Next, take the anti-derivative of the integrand and replace u with the original expression, adding the constant
out front of the integral. Next, take the anti-derivative of the integrand and replace u with the original expression, adding the constant  to the answer.
to the answer.
The specific steps are as follows:
1. 
2.
3. 
4. 
5. 
6. 
7. 
8. 
9. 
To solve the integral, we have to simplify it by using a variable u to substitute for a variable of x.
For this problem, we will let u replace the expression 
Next, we must take the derivative of u. Its derivative is 
Next, solve this equation for dx so that we may replace it in the integral.
Plug 



The 




The specific steps are as follows:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of u. Its derivative is
. Next, we must take the derivative of u. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral, leaving behind a
in the integral, leaving behind a  . We can pull the
. We can pull the  out front of the integral. Next, take the anti-derivative of the integrand and replace
out front of the integral. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2.  =
=
3. 
4.
5. 
6. 
7. 
8. 
To solve the integral, we have to simplify it by using a variable 














1.
2. 
3.
4.
5.
6.
7.
8.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of
. Next, we must take the derivative of  . Its derivative is
. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral, leaving behind a
in the integral, leaving behind a  . Next, take the anti-derivative of the integrand and replace
. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
To solve the integral, we have to simplify it by using a variable 














1.
2.
3.
4.
5.
6.
7.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of
. Next, we must take the derivative of  . Its derivative is
. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral, leaving behind a
in the integral, leaving behind a  . We can pull the
. We can pull the  out front of the integral. Next, take the anti-derivative of the integrand and replace
out front of the integral. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
To solve the integral, we have to simplify it by using a variable 















1.
2.
3.
4.
5.
6.
7.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of
. Next, we must take the derivative of  . Its derivative is
. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral, leaving behind a
in the integral, leaving behind a  . We can pull the
. We can pull the  out front of the integral. Next, take the anti-derivative of the integrand and replace
out front of the integral. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
To solve the integral, we have to simplify it by using a variable 















1.
2.
3.
4.
5.
6.
7.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of
. Next, we must take the derivative of  . Its derivative is
. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral. Next, take the anti-derivative of the integrand and replace
in the integral. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
To solve the integral, we have to simplify it by using a variable 













1.
2.
3.
4.
5.
6.
7.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of
. Next, we must take the derivative of  . Its derivative is
. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral. Next, take the anti-derivative of the integrand and replace
in the integral. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
To solve the integral, we have to simplify it by using a variable 













1.
2.
3.
4.
5.
6.
7.
8.
Compare your answer with the correct one above
Solve the following integral using substitution:

Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable  to substitute for a variable of
to substitute for a variable of  . For this problem, we will let u replace the expression
. For this problem, we will let u replace the expression  . Next, we must take the derivative of
. Next, we must take the derivative of  . Its derivative is
. Its derivative is  . Next, solve this equation for
. Next, solve this equation for  so that we may replace it in the integral. Plug
so that we may replace it in the integral. Plug  in place of
in place of  and
and  in place of
in place of  into the original integral and simplify. The
into the original integral and simplify. The  in the denominator cancels out the remaining
in the denominator cancels out the remaining  in the integral, leaving behind a
in the integral, leaving behind a  . We can pull the
. We can pull the  out front of the integral. Next, take the anti-derivative of the integrand and replace
out front of the integral. Next, take the anti-derivative of the integrand and replace  with the original expression, adding the constant
with the original expression, adding the constant  to the answer. The specific steps are as follows:
to the answer. The specific steps are as follows:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
To solve the integral, we have to simplify it by using a variable 















1.
2.
3.
4.
5.
6.
7.
8.
Compare your answer with the correct one above
Solve:

Solve:
To integrate, we must make the following substitution:

Rewriting the integral in terms of u and integrating, we get

The following rule was used for integration:

Replacing u with our original x term, we get

To integrate, we must make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used for integration:
Replacing u with our original x term, we get
Compare your answer with the correct one above
Use u-subtitution to fine

Use u-subtitution to fine
Let 
Then 
Now we can subtitute

Now we substitute back

Let
Then
Now we can subtitute
Now we substitute back
Compare your answer with the correct one above
Evaluate 
Evaluate
We can use substitution for this integral.
Let  ,
,
then  .
.
Multiplying this last equation by  , we get
, we get  .
.
Now we can make our substitutions
 . Start
. Start
 . Swap out
. Swap out  with
with  , and
, and  with
with  . Make sure you also plug the bounds on the integral into
. Make sure you also plug the bounds on the integral into  for
for  to get the new bounds.
to get the new bounds.
 . Factor out the
. Factor out the  .
.
 . Integrate (absolute value signs are not needed since
. Integrate (absolute value signs are not needed since  .)
.)
 . Evaluate
. Evaluate
 .
.
We can use substitution for this integral.
Let 
then 
Multiplying this last equation by 

Now we can make our substitutions














Compare your answer with the correct one above
This is a u-substitution integral. We need to substitute the new function, which is modifying our base function (the exponential).
 , but instead of that, our problem is
, but instead of that, our problem is  . We can solve this integral by completing the substitution.
. We can solve this integral by completing the substitution.

Now, we can replace everything in our integrand and rewrite in terms of our new variables:

 .
.
Remember to plug your variable back in and include the integration constant since we have an indefinite integral.
This is a u-substitution integral. We need to substitute the new function, which is modifying our base function (the exponential).


Now, we can replace everything in our integrand and rewrite in terms of our new variables:

Remember to plug your variable back in and include the integration constant since we have an indefinite integral.
Compare your answer with the correct one above
This is a u-substitution integral. We need to choose the following substitutions:

Now, we can replace our original problem with our new variables:


In the last step, we need to plug in our original function and add the integration constant.
This is a u-substitution integral. We need to choose the following substitutions:
Now, we can replace our original problem with our new variables:
In the last step, we need to plug in our original function and add the integration constant.
Compare your answer with the correct one above
This is a hidden u-substitution problem! Because we have a function under our square root, we cannot just simply integrate it. Therefore, we need to choose the function under the square root as our substitution variable!

Now, let us rewrite our original equation in terms of our new variable!


 .
.
This is a hidden u-substitution problem! Because we have a function under our square root, we cannot just simply integrate it. Therefore, we need to choose the function under the square root as our substitution variable!
Now, let us rewrite our original equation in terms of our new variable!

Compare your answer with the correct one above


