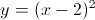Algebra - How to graph a quadratic function

What is the equation of a parabola with vertex and -intercept ?

$y = -\frac{1}{2} x^{2} +4x - 7$

$y = -\frac{1}{2} x^{2} -4x - 7$

$y = \frac{1}{2} x^{2} -4x - 7$

$y = \frac{1}{2} x^{2} -8x - 7$

$y = \frac{1}{2} x^{2} +8x - 7$

Explanation

From the vertex, we know that the equation of the parabola will take the form $y = a (x - 4) ^{2}+ 1$ for some .

To calculate that , we plug in the values from the other point we are given, , and solve for :

$y = a (x - 4)^{2} + 1$

$-7= a \cdot (0 - 4)^{2} + 1$

$-7= a \cdot (- 4)^{2} + 1$

$a = -\frac{1}{2}$

Now the equation is $y = -\frac{1}{2} (x - 4)^{2} + 1$ . This is not an answer choice, so we need to rewrite it in some way.

Expand the squared term:

$y = -\frac{1}{2} (x^{2} -8x + 16) + 1$

Distribute the fraction through the parentheses:

$y = -\frac{1}{2} x^{2} +4x - 8 + 1$

Combine like terms:

$y = -\frac{1}{2} x^{2} +4x - 7$

For the graph below, match the graph b with one of the following equations:

$y= x^{2}$

$y = (x-2)^{2}$

$y = (x+3)^{2}$

$y = -(x-2)^{2} -2$

Parabola

$y = (x+3)^{2}$

$y = x^{2}$

$y = (x-2)^{2}$

$y = -(x-2)^{2} - 2$

None of the above

Explanation

Starting with $y = x^{2}$

$(x-2)^{2}$ moves the parabola $x^{2}$ by units to the right.

Similarly $(x+3)^{2}$ moves the parabola by units to the left.

Hence the correct answer is option .

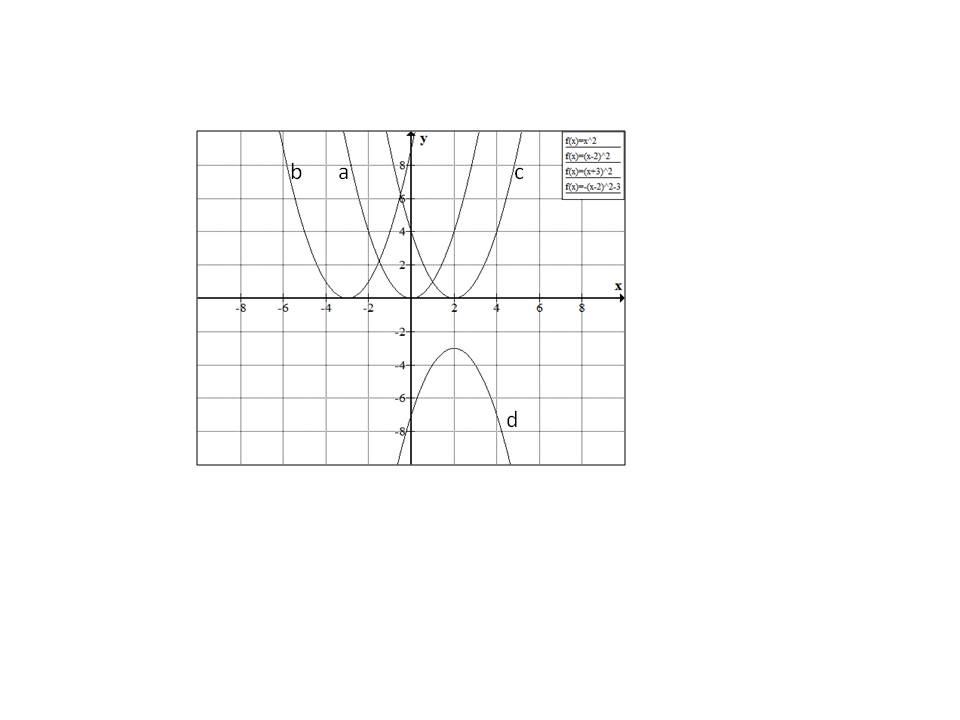
Which of the following graphs matches the function ?

Graph

Graph1

Graph2

Graph3

Graph4

Explanation

Start by visualizing the graph associated with the function :

Graph5

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of looks like this:

Graph6

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function :

Graph

What is the vertex of the function $\small f(x)=2(x-4)^2+7$ ? Is it a maximum or minimum?

$\small (4,7)$ ; minimum

$\small (4,7)$ ; maximum

$\small (-4,7)$ ; minimum

$\small (-4,7)$ ; maximum

Explanation

The equation of a parabola can be written in vertex form: $\small f(x)=a(x-h)^2+k$ .

The point $\small (h,k)$ in this format is the vertex. If $\small a$ is a postive number the vertex is a minimum, and if $\small a$ is a negative number the vertex is a maximum.

$\small f(x)=2(x-4)^2+7$

In this example, $\small a=2$ . The positive value means the vertex is a minimum.

$\small h=4\ \text{and}\ k=7$

$\small (h,k)=(4,7)$

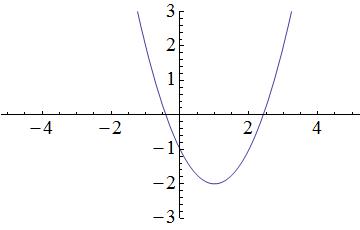
Which of the graphs best represents the following function?

$f(x)=\frac{9}{10}x^2-7x+2$

Graph_parabola_

Graph_cube_

Graph_exponential_

None of these

Graph_line_

Explanation

$f(x)=\frac{9}{10}x^2-7x+2$

The highest exponent of the variable term is two (). This tells that this function is quadratic, meaning that it is a parabola.

The graph below will be the answer, as it shows a parabolic curve.

Graph_parabola_

What is the minimum possible value of the expression below?

$3x^{2}+6x-10$

The expression has no minimum value.

Explanation

We can determine the lowest possible value of the expression by finding the -coordinate of the vertex of the parabola graphed from the equation $y=3x^{2}+6x-10$ . This is done by rewriting the equation in vertex form.