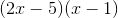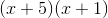A perfect square trinomial takes the form

,

where

Since , for to be a perfect square,

.

This makes the correct choice.

The first step in setting up our binomial is to figure out our possible leading terms. In this case, the only reasonable factors of are :

Next, find the factors of . In this case, we could have or . Since the factor on our leading term is , and no additive combination of and can create , we know that our factors must be .

Note that since the last term in the ordered trinomial is negative, the factors must have different signs.

Therefore, we have two possibilities, or .

Let's solve for both, and check against the original triniomial.

Thus, our factors are and .

For the trinomial to be factorable, we would have to be able to find two integers with product 36 and sum ; that is, would have to be the sum of two integers whose product is 36.

Below are the five factor pairs of 36, with their sum listed next to them. must be one of those five sums to make the trinomial factorable.

1, 36: 37

2, 18: 20

3, 12: 15

4, 9: 13

6, 6: 12

Of the five choices, only 16 is not listed, so if , then the polynomial is prime.

The first step in setting up our binomial is to figure out our possible leading terms. In this case, the only reasonable factors of are :

Next, find the factors of . In this case, we could have or . Either combination can potentially produce , so the signage is important here.

Note that since the last term in the ordered trinomial is positive, both factors must have the same sign. Further, since the middle term in the ordered triniomial is negative, we know the signs must both be negative.

Therefore, we have two possibilities, or .

Let's solve for both, and check against the original triniomial.

Thus, our factors are and .

We are looking to factor this quadratic trinomial into two factors, where the question marks are to be replaced by two integers whose product is and whose sum is .

We need to look at the factor pairs of in which the negative number has the greater absolute value and the sum is :

None of these pairs have the desired sum, so the polynomial is prime.

To factor the trinomial, its general form given by , we must find factors of the product that when added together give us .

For our trinomial, and . The two factors that fit the above rule are and , because and .

Using the two factors, we can rewrite the term as a sum of the two factors added together and multiplied by x:

Now, we must factor by grouping, which means we group the first two terms, and the last two terms, and factor them:

Note that after we factored the two groups of terms, what remained inside the parentheses is identical for the two groups.

Simplifying further, we get

, which is our final answer.

When we factor, we have to remember to check the signs in the trinomial. In this case, we have minus 7 and plus 12. That automatically tells us the signs in the factors must be the same, both "-" signs.

Next, we ask ourselves what are the factors of 12? We get 2 & 6, 1 & 12, and 4 & 3.

Then, we ask ourselves, which of these when added/subtracted in a given order, will give us 7? The answer is 4 and 3! So we place these in the parentheses with the 's that we know go there so it looks like

We can factor this trinomial using the FOIL method backwards. This method allows us to immediately infer that our answer will be two binomials, one of which begins with and the other of which begins with . This is the only way the binomials will multiply to give us .

The next part, however, is slightly more difficult. The last part of the trinomial is , which could only happen through the multiplication of 1 and 2; since the 2 is negative, the binomials must also have opposite signs.

Finally, we look at the trinomial's middle term. For the final product to be , the 1 must be multiplied with the and be negative, and the 2 must be multiplied with the and be positive. This would give us , or the that we are looking for.

In other words, our answer must be

to properly multiply out to the trinomial given in this question.

To factor trinomials like this one, we need to do a reverse FOIL. In other words, we need to find two binomials that multiply together to yield .

Finding the "first" terms is relatively easy; they need to multiply together to give us , and since only has two factors, we know the terms must be and . We now have  , and this is where it gets tricky.

The second terms must multiply together to give us , and they must also multiply with the first terms to give us a total result of . Many terms fit the first criterion. , , and all multiply to yield . But the only way to also get the "" terms to sum to is to use . It's just like a puzzle!

Rewrite this as

Use the -method by splitting the middle term into two terms, finding two integers whose sum is 1 and whose product is ; these integers are , so rewrite this trinomial as follows:

Now, use grouping to factor this: