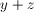ACT Math - How to find f(x)

An outpost has the supplies to last 2 people for 14 days. How many days will the supplies last for 7 people?

$\dpi{100} \small 4$

$\dpi{100} \small 7$

$\dpi{100} \small 5$

$\dpi{100} \small 10$

$\dpi{100} \small 9$

Explanation

Supplies are used at the rate of $\dpi{100} \small \frac{Supplies}{Days\times People}$ .

Since the total amount of supplies is the same in either case, $\dpi{100} \small \frac{1}{14\times 2}=\frac{1}{7\times \ (&hash;\ of\ days)}$ .

Solve for days to find that the supplies will last for 4 days.

When written in symbols, “The square of the sum of and equals ” is represented as:

Explanation

“The square of the sum” means that the summation of the terms is done first, and that summation is squared, which corresponds to the term .

A book binding company charges a fixed fee of $2.25 to bind a book and an additional $0.15 per page. Which equation accurately calculates the cost, C, of a book with p number of pages?

Explanation

The company's binding process incorporates a fixed fee; therefore, we must use the formula for a linear equation:

The fixed fee means that the consumer pays a single fee of $2.25 to bind the book regardless of how many pages that book has; thus, the fixed fee is represented by the y-intercept, or b, of the equation. The problem states that each page will cost an additional $0.15 per page, which varies with depending on the number of pages in the book. The page cost is represented by the slope, m, of the equation. In order to calculate the total cost, , you must multiply the number of pages, p, by $0.15 and add the fixed cost of $2.25; therefore, the following equation accurately models the cost of binding a book:

Find

$f(x)=|x^{2}+4x-127|$

Explanation

Simply plug 6 into the equation and don't forget the absolute value at the end.

absolute value = 67

If and , then

Explanation

To answer this question, we need to understand exactly what actually means.

We start from the inside of the parentheses and work outwards. Therefore, we first solve for using the equation for provided for us. So, for this data:

Therefore, . We now take that answer and plug it in for the value within . So, for this data:

Therefore, the answer to is .

If , what does equal?

Explanation

For a question like this, treat it just like you would the use of a numeric value for evaluating your function. All you do is “plug in” . Thus, for this function, you get:

Next, you just need to distribute everything correctly:

If , what is ?

Explanation

For a question like this, treat it just like you would the use of a numeric value for evaluating your function. All you do is “plug in” . Thus, for this function, you get:

From here, you merely need to distribute correctly!

Given the functions and , what is when ?

Explanation

In order to find , work from the inside out. In other words, begin by finding , or since

Now, seeing as . Substitute for in in order to find the answer.

For which value of are the following two functions equal?

$F(x)=2x+3^x+\frac{9x}{3}$

$G(x)=\frac{2^x+4^x}{2}-4x-5x+1$

Explanation

It is important to follow the order of operations for this equation and find a solution that satisfies both F(x) and G(x).

Recall the order of operations is PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.

The correct answer is 4 because

F(x) = 2_x_ + 3_x_ + (9_x_/3) = 2(4) + 34 + ((9 * 4)/3) = 101, and

G(x) = (((24 + 44)/2) - 4 * 4) – 5(4) + 1 = 101.

If the average of two numbers is $\dpi{100} \small 3y$ and one of the numbers is $\dpi{100} \small y+z$ , what is the other number, in terms of $\dpi{100} \small y$ and $\dpi{100} \small z$ ?

$\dpi{100} \small 5y-z$

$\dpi{100} \small 5y+z$

$\dpi{100} \small y+z$

$\dpi{100} \small 3y+z$

$\dpi{100} \small 4y-z$

Explanation

The average is the sum of the terms divided by the number of terms. Here you have $\dpi{100} \small y+z$ and the other number which you can call $\dpi{100} \small x$ . The average of $\dpi{100} \small x$ and $\dpi{100} \small y+z$ is $\dpi{100} \small 3y$ . So $\dpi{100} \small 3y=\frac{(x+y+z)}{2}$