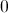ACT Math - How to find absolute value

Which of the following sentences is represented by the equation

The absolute value of the sum of a number and seven is three less than the number.

The absolute value of the sum of a number and seven is three greater than the number.

The sum of three and the absolute value of the sum of a number is three greater than the number.

The sum of three and the absolute value of the sum of a number is three less than the number.

None of the other responses are correct.

Explanation

is the absolute value of , which in turn is the sum of a number and seven and a number. Therefore, can be written as "the absolute value of the sum of a number and seven". Since it is equal to , it is three less than the number, so the equation that corresponds to the sentence is

"The absolute value of the sum of a number and seven is three less than the number."

Evaluate for :

$\left | 4x - 1.4 \right | + \left | x^{2} - 1 \right |$

Explanation

Substitute 0.6 for :

$\left | 4x - 1.4 \right | + \left | x^{2} - 1 \right |$

$= \left | 4 \cdot 0.6 - 1.4 \right | + \left | 0.6^{2} - 1 \right |$

$= \left | 2.4 - 1.4 \right | + \left | 0.36 - 1 \right |$

$= \left | 1 \right | + \left | -0.64 \right |$

Define an operation $\blacktriangledown$ as follows:

For all real numbers ,

$a \blacktriangledown b= \frac{a+1}{\left | a\right |+ \left | b\right |}$

Evaluate: $\frac{4}{5} \blacktriangledown \left (-\frac{4}{5} \right )$ .

$1 \frac{1}{8}$

The expression is undefined.

$\frac{5}{8}$

None of the other responses is correct.

Explanation

$a \blacktriangledown b= \frac{a+1}{\left | a\right |+ \left | b\right |}$ , or, equivalently,

$a \blacktriangledown b=\left ( a+1 \right ) \div ( | a |+ | b | )$

$\frac{4}{5} \blacktriangledown \left (-\frac{4}{5} \right )=\left ( \frac{4}{5}+1 \right ) \div \left (\left| \frac{4}{5} \right |+ \left |- \frac{4}{5}\right | \right )$

$= \frac{9}{5} \div \left ( \frac{4}{5} +\frac{4}{5} \right )$

$= \frac{9}{5} \div \frac{8}{5}$

$= \frac{9}{5} \times \frac{5}{8}$

$= \frac{9}{8}$

$=1 \frac{1}{8}$

Find the absolute value of the following when x = 2,

$\left | \frac{x^3-12}{2}\right |$

Explanation

$2^{3}=8$

and $\frac{-4}{2}=-2$

It is important to know that the absolute value of something is always positive so the absolute value of is

2 is your answer.

$\left | 7 - 2\right | - \left | 4 - 8\right | =?$

Explanation

Absolute value is the key here. Absolute value means the number's distance from zero. So we must account for that. Therefore $\left | 4-8\right |$ $= \left | -4\right | = 4$ .