8th Grade Math - Give Examples of Linear Equations: CCSS.Math.Content.8.EE.C.7a

Select the option that describes the solution(s) for the following equation:

One solution

Infinitely many solutions

No solution

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

$\frac{\begin{array}[b]{r}15y=5y+70\ -5y -5y\ \ \ \ \ \ \ \end{array}}{10y=70}$

$\frac{10y}{10}=\frac{70}{10}$

This equation equals a single value; thus, the correct answer is one solution.

Select the option that describes the solution(s) for the following equation:

Infinitely many solutions

One solution

No solution

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

This equation equals a statement that is always true; thus, the correct answer is infinitely many solutions.

Select the option that describes the solution(s) for the following equation:

One solution

No solution

Infinitely many solutions

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

$\frac{\begin{array}[b]{r}-9x=-10x+8\ +10x\ +10x\ \ \ \ \ \end{array}}{12=3d}$

This equation equals a single value; thus, the correct answer is one solution.

Select the option that describes the solution(s) for the following equation:

No solution

One solution

Infinitely many solutions

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

$\frac{\begin{array}[b]{r}9x=9x+27\ -9x -9x\ \ \ \ \ \ \ \end{array}}{0=27}$

This equation equals a false statement; thus, the correct answer is no solution.

Select the option that describes the solution(s) for the following equation:

No solution

One solution

Infinitely many solutions

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

$\frac{\begin{array}[b]{r}2x=2x+5\ -2x -2x\ \ \ \ \ \end{array}}{0=5}$

This equation equals a false statement; thus, the correct answer is no solution.

How many solutions does the equation below have?

No solutions

One

Two

Three

Infinite

Explanation

When finding how many solutions an equation has you need to look at the constants and coefficients.

The coefficients are the numbers alongside the variables.

The constants are the numbers alone with no variables.

If the coefficients are the same on both sides then the sides will not equal, therefore no solutions will occur.

Use distributive property on the right side first.

No solutions

Solve the equation: $\left | 2x+3\right |=-1$

No solution

$\pm1$

Explanation

Notice that the end value is a negative. Any negative or positive value that is inside an absolute value sign must result to a positive value.

If we split the equation to its positive and negative solutions, we have:

Solve the first equation.

The answer to is:

Solve the second equation.

The answer to is:

If we substitute these two solutions back to the original equation, the results are positive answers and can never be equal to negative one.

The answer is no solution.

Solve: $\frac{x^2-1}{x-1} = 2$

$\textup{No solution.}$

$\pm1$

Explanation

First factorize the numerator.

Rewrite the equation.

$\frac{(x-1)(x+1)}{x-1} = 2$

The terms can be eliminated.

Subtract one on both sides.

However, let's substitute this answer back to the original equation to check whether if we will get as an answer.

$\frac{(1)^2-1}{1-1} = 2$

Simplify the left side.

$\frac{0}{0}=2$

The left side does not satisfy the equation because the fraction cannot be divided by zero.

Therefore, is not valid.

The answer is: $\textup{No solution.}$

Select the option that describes the solution(s) for the following equation:

One solution

Infinitely many solutions

No solution

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

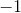
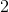
$\frac{\begin{array}[b]{r}14d+12=17d\ -14d\ \ \ \ \ \ \ -14d\end{array}}{12=3d}$

$\frac{12}{3}=\frac{3d}{3}$

This equation equals a single value; thus, the correct answer is one solution.

Select the option that describes the solution(s) for the following equation:

Infinitely many solutions

One solution

No solution

Explanation

Let's begin by discussing our answer choices:

In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,

In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,

In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example,

To answer this question, we can solve the equation:

This equation equals a statement that is always true; thus, the correct answer is infinitely many solutions.

Give Examples of Linear Equations: CCSS.Math.Content.8.EE.C.7a

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation