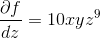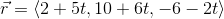Multivariable Calculus
Help Questions
Multivariable Calculus › Multivariable Calculus
Find the equation of the tangent plane to 

Explanation
First, we need to find the partial derivatives in respect to 





Remember that the general equation for a tangent plane is as follows:
Now lets apply this to our problem
Determine the length of the curve 

Explanation
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Write down the equation of the line in vector form that passes through the points 

Explanation
Remember the general equation of a line in vector form:



Lets apply this to our problem.
Distribute the
Now we simply do vector addition to get
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Write down the equation of the line in vector form that passes through the points 

Explanation
Remember the general equation of a line in vector form:



Lets apply this to our problem.
Distribute the
Now we simply do vector addition to get
Calculate the curl for the following vector field.
Explanation
In order to calculate the curl, we need to recall the formula.
where 


Now lets apply this to out situation.
Thus the curl is
Calculate the curl for the following vector field.
Explanation
In order to calculate the curl, we need to recall the formula.
where 


Now lets apply this to out situation.
Thus the curl is