How to use a Venn Diagram
Help Questions
ISEE Upper Level Quantitative Reasoning › How to use a Venn Diagram

In the above Venn diagram, the universal set is defined as 

Explanation














In the above Venn diagram, the universal set is defined as 
What is 
Explanation







In a group of plants, 


Explanation
Based on the information, you can draw the following Venn Diagram:

It is very easy to solve for the number of plants that have green leaves but not large ones. This is merely 
In a group of 



Cannot be determined
Explanation
Based on the information given, you can draw the following Venn Diagram:

Now, you must begin by solving for 






Now, we can find the number of people with only books by subtracting 


In a group of 



No answer possible
Explanation
Based on the information given, you can draw the following Venn Diagram:

To solve this, remember that the total number of values in the two circles is:
(We must do this because of the overlap. You need to subtract out one instance of that overlap.)
If we assign the value 

In the above Venn diagram, the universal set is defined as 
What is 
Explanation








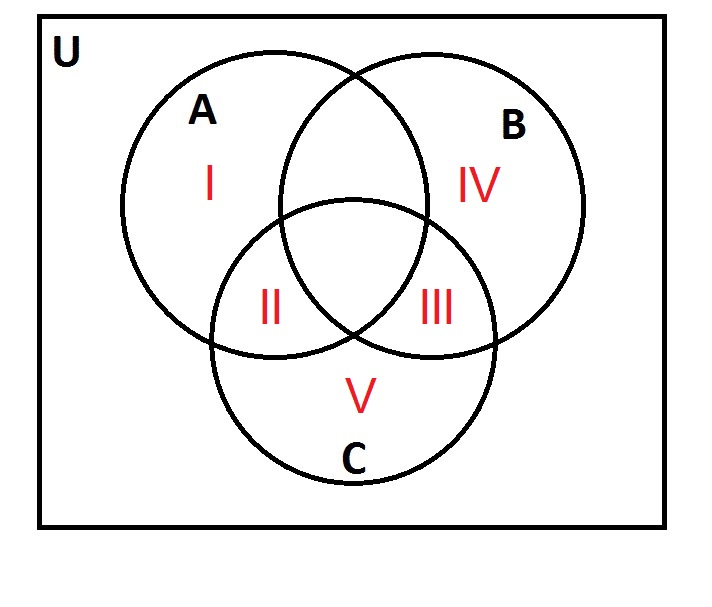
Examine the above Venn diagram. Let 



James Abram Garfield was born in Ohio in 1831. In which region would he fall?
V
I
II
III
IV
Explanation
Carter would not fall in set A, since he was not a President born in Virginia.
He would not fall in B, since he was born before 1850.
He would fall in C, since his first name is James.
He would fall in the region included in set C, but not A or B - this is Region V.

Examine the above Venn diagram. Let 



James Earl Carter was born in Georgia in 1924. In which region would he fall?
III
I
II
IV
V
Explanation
Carter would not fall in set A, since he was not a President born in Virginia.
He would fall in B, since he was born after 1850.
He would fall in C, since his first name is James.
He would fall in the region included in sets B and C, but not A - this is Region III.

Examine the above Venn diagram. Let universal set 
Let 


Which of the following would be a subset of the set represented by the shaded region in the diagram?
Note: for purposes of this question, "Y" is considered a consonant.
{plateau, portmanteau, calliope, marionette, taco}
{tomato, potato, ravine, cabana, marine}
{autistic, estrogen, ideology, opal, understand}
{autism, enough, ideals, occult, unduly}
{apnea, esoterica, irradiate, opulence, uvula}
Explanation
The subset must comprise words that fall inside sets 


Of the given choices, the only set whose elements fit this description is {plateau, portmanteau, calliope, marionette, taco}.

In the above Venn diagram, the universal set is defined as 

Explanation


























































