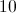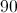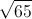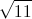How to find the length of the hypotenuse of a right triangle : Pythagorean Theorem
Help Questions
ISEE Upper Level Quantitative Reasoning › How to find the length of the hypotenuse of a right triangle : Pythagorean Theorem
In a right triangle, two sides have length 

Explanation
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 


Refer to the above diagram, which depicts a right triangle. What is the value of 
Explanation
By the Pythagorean Theorem, which says 


Simply
If a right triangle has a base of 

Explanation
To solve this problem, we are going to use the Pythagorean Theorom, which states that 
We know that this particular right triangle has a base of 



Next, we evaluate the expoenents:
Then, 
To solve for 


The legs of a right triangle are equal to 4 and 5. What is the length of the hypotenuse?
Explanation
If the legs of a right triangle are 4 and 5, to find the hypotenuse, the following equation must be used to find the hypotenuse, in which c is equal to the hypotenuse:
In a right triangle, two sides have lengths 5 centimeters and 12 centimeters. Give the length of the hypotenuse.
Explanation
This triangle has two angles of 45 and 90 degrees, so the third angle must measure 45 degrees; this is therefore an isosceles right triangle.
By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let 


If a right triangle has a base of 

Explanation
To solve this problem, we must utilize the Pythagorean Theorom, which states that:
We know that the base is 





Next we evaluate the exponents:
Now we add them together:
Then, 


In a right triangle, the legs are 7 feet long and 12 feet long. How long is the hypotenuse?
Explanation
The pythagorean theory should be used to solve this problem.
In a right triangle, if the base of the triangle is 3, and the height is 5, what must be the length of the hypotenuse?
Explanation
Write the formula of the Pythagorean Theorem.
The value of 
Substitute the side lengths.
Square root both sides.
The answer is:
What is the hypotenuse of a right triangle with sides 5 and 8?
undefined
Explanation
According to the Pythagorean Theorem, the equation for the hypotenuse of a right triangle is 



In a rectangle, the width is 6 feet long and the length is 8 feet long. If a diagonal is drawn through the rectangle, from one corner to the other, how many feet long is that diagonal?
Explanation
Given that a rectangle has all right angles, drawing a diagonal will create a right triangle the legs are each 6 feet and 8 feet.
We know that in a 3-4-5 right triangle, when the legs are 3 feet and 4 feet, the hypotenuse will be 5 feet.
Given that the legs of this triangle are twice as long as those in the 3-4-5 triangle, it follows that the hypotense will also be twice as long.
Thus, the diagonal in through the rectangle creates a 6-8-10 triangle. 10 is therefore the length of the diagonal.