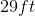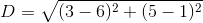You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the arms are 1.5 feet, what is the perimeter of the base of your new bookshelf?

To find the perimeter of a bookshelf, we need to add up the lengths of the sides.

We know the two bases, we just need to add the lengths of the arms.

So, our answer is 8ft

Area of a triangle can be determined using the equation:

For the sake of simplicity, we will assume that the second square has sidelength 1; Then its perimeter is , and its area is .

The perimeter of the first square is , and its sidelength is . The area of this square is therefore .

The ratio of the areas is therefore .

The fence is going around the garden, so this is a perimeter problem.

To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, , we can solve for the area of both of our rectangles

To find our final answer, we need to add the areas together.

A rectangular postage stamp has a width of 3 cm and a height of 12 cm. Find the area of the stamp.

To find the area of a rectangle, we must perform the following:

Where l and w are our length and width.

This means we need to multiply the given measurements. Be sure to use the right units!

And we have our answer. It must be centimeters squared, because we are dealing with area.

Area of a triangle can be determined using the equation:

The fence is going around the garden, so this is a perimeter problem.

To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, , we can solve for the area of both of our rectangles

To find our final answer, we need to add the areas together.

The length of a line segment can be determined using the distance formula: