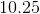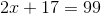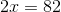Understand and apply concepts of equations
Help Questions
HiSET › Understand and apply concepts of equations
Solve for 
Explanation
To solve for 

First, take the reciprocal of both sides:
Multiply both sides by 
Distribute on the right:
Subtract 1 from both sides, rewriting 1 as 

the correct response.
Solve the following equation:
Explanation
The first step to solving an equation where 
Now that the radical is isolated, clear the radical by raising both sides to the power of 3. Note:
Now we want to isolate the 
Finally, divide both sides by 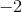

Solve for 
Explanation
To solve for 

First, take the reciprocal of both sides:
Multiply both sides by 
Distribute on the right:
Subtract 1 from both sides, rewriting 1 as 

the correct response.
What is 25% of 
Explanation
Solve for 
by isolating 
First, subtract 17 from both sides:
Now, divide both sides by 2:
One way to find 25% of this value is to multiply 41 by 25 and divide by 100:

the correct choice.
What is the vertex of the following quadratic polynomial?
Explanation
Given a quadratic function
the vertex will always be

Thus, since our function is



We plug these variables into the formula to get the vertex as

Hence, the vertex of
is

What is 25% of 
Explanation
Solve for 
by isolating 
First, subtract 17 from both sides:
Now, divide both sides by 2:
One way to find 25% of this value is to multiply 41 by 25 and divide by 100:

the correct choice.
What is the vertex of the following quadratic polynomial?
Explanation
Given a quadratic function
the vertex will always be

Thus, since our function is



We plug these variables into the formula to get the vertex as

Hence, the vertex of
is

Solve the following equation:
Explanation
The first step to solving an equation where 
Now that the radical is isolated, clear the radical by raising both sides to the power of 3. Note:
Now we want to isolate the 
Finally, divide both sides by 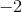

Which of the following expressions represents the discriminant of the following polynomial?
Explanation
The discriminant of a quadratic polynomial
is given by

Thus, since our quadratic polynomial is




Plugging these values into the discriminant equation, we find that the discriminant is

Which of the following expressions represents the discriminant of the following polynomial?
Explanation
The discriminant of a quadratic polynomial
is given by

Thus, since our quadratic polynomial is




Plugging these values into the discriminant equation, we find that the discriminant is














![\sqrt[3]{5-2x}+5=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072122/gif.latex)

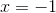
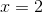

![x=\sqrt[3]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072121/gif.latex)
![\sqrt[3]{5-2x}+5=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072123/gif.latex)
![\sqrt[3]{5-2x}+5-5=4-5](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1082121/gif.latex)
![\sqrt[3]{5-2x}=-1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072124/gif.latex)

![(\sqrt[3]{5-2x})^3=(-1)^3](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1082123/gif.latex)