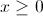Solving Inequalities
Help Questions
Math › Solving Inequalities
What is the solution set for 
Explanation
Start by finding the roots of the equation by changing the inequality to an equal sign.
Now, make a number line with the two roots:

Pick a number less than 
For 


Next, pick a number between 
For 


Finally, pick a number greater than 
For 


Thus, the solution set for this inequality is 
Solve for 
Explanation
The first step is to distribute (multiply) through the parentheses:
Then subtract 
Next, subtract the 12:
Finally, divide by two:
Solve the inequality:
Explanation
Solve this inequality.
Explanation
Split the inequality into two possible cases as follows, based on the absolute values.
First case:
Second case:
Let's find the inequality of the first case.
Multiply both sides by x + 6.
Subtract x from both sides, then subtract 3 from both sides.
Divide both sides by 3.
Let's find the inequality of the second case.
Multiply both sides by x + 6.
Simplify.
Add x to both sides, then subtract 3 from both sides.
Divide both sides by 5.
So the range of x-values is 

Solve for 
Explanation
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 

Solve the inequality:
Explanation
Add 26 on both sides.
Divide by two on both sides.
The answer is:
Solve the inequality:
Explanation
Add 
The inequality becomes:
Subtract 8 from both sides.
Divide by 18 on both sides.
The answer is:
Solve for 
Explanation
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 

Solve for 
Explanation
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 

Solve the inequality:
Explanation
Subtract nine from both sides.
Divide by negative 3 on both sides. We will need to switch the sign.
The answer is: