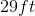Squares

Help Questions

Math › Squares

Questions 1 - 10

The lengths of the sides of ten squares form an arithmetic sequence. One side of the smallest square measures sixty centimeters; one side of the second-smallest square measures one meter.

Give the area of the largest square, rounded to the nearest square meter.

18 square meters

16 square meters

20 square meters

22 square meters

24 square meters

Explanation

Let $a_{n}$ be the lengths of the sides of the squares in meters. $a_{1} = 60 \div 100 = 0.6$ and $a_{2} = 1$ , so their common difference is

The arithmetic sequence formula is

$a_{n} = a_{1} + (n-1)d$

The length of a side of the largest square - square 10 - can be found by substituting $a_{1} = 0.6, n= 10, d = 0.4$ :

$a_{10} =0.6+ (10-1) 0.4 = 0.6 + 9 (0.4) = 0.6 + 3.6 = 4.2$

The largest square has sides of length 4.2 meters, so its area is the square of this, or $A = 4.2^{2} = 17.64$ square meters.

Of the choices, 18 square meters is closest.

Which is the greater quantity?

(a) The sidelength of a square with area square inches.

(b) The sidelength of a square with perimeter inches.

(a) is greater.

(b) is greater.

(a) and (b) are equal.

It is impossible to tell which is greater from the information given.

Explanation

The sidelength of a square is the square root of its area and one-fourth of its perimeter, so:

(a) A square with area square inches has sidelength $\sqrt{225} = 15$ inches.

(b) A square with perimeter inches has sidelength $50 \div 4 = 12.5$ inches.

(a) is the greater quantity.

If the diagonal of a square is $19\sqrt2$ , what is the area of the square?

Explanation

The diagonal of a square is also the hypotenuse of a triangle whose legs are the sides of the square.

Thus, from knowing the length of the diagonal, we can use Pythagorean's Theorem to figure out the side lengths of the square.

$\text{Diagonal}^2=\text{side length}^2+\text{side length}^2$

$\text{Diagonal}^2=2(\text{side length})^2$

$(\text{side length})^2=\frac{\text{Diagonal}^2}{2}$

$\text{side length}=\frac{\text{Diagonal}}{\sqrt2}$

We can now find the side length of the square in question.

$\text{side length}=\frac{19\sqrt2}{\sqrt2}$

Simplify.

$\text{side length}=19$

Now, recall how to find the area of a square:

$\text{Area}=(\text{side length})^2$

For the square in question,

$\text{Area }=19 ^2$

Solve.

$\text{Area }=361$

If the diagonal of a square is $6\sqrt2$ , what is the area of the square?

Explanation

The diagonal of a square is also the hypotenuse of a right triangle that has the side lengths of the square as its legs.

We can then use the Pythgorean Theorem to write the following equations:

$\text{Diagonal}=\sqrt{\text{side length}^2+\text{side length}^2}$

$\text{Diagonal}=\sqrt{2(\text{side length})^2}$

$\text{Diagonal}=(\text{side length})\sqrt2$

$\text{Side length}=\frac{\text{Diagonal}}{\sqrt2}$

Now, use this formula and substitute using the given values to find the side length of the square.

$\text{Side length}=\frac{6\sqrt2}{\sqrt2}$

Simplify.

$\text{Side length}=6$

Now, recall how to find the area of a square.

$\text{Area}=(\text{side length})^2$

For this square in question,

$\text{Area}=6^2$

Solve.

$\text{Area}=36$

Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is by

Explanation

The fence is going around the garden, so this is a perimeter problem.

What is the perimeter of a square with area 196 square inches?

$56 ; \textrm{in}$

$28 ; \textrm{in}$

$112 ; \textrm{in}$

$64; \textrm{in}$

It cannot be determined from the information given.

Explanation

A square with area 196 square inches has sidelength $\sqrt{196} = 14$ inches, and therefore has perimeter $4 \cdot 14 = 56$ inches

What is the length of a rectangular room with a perimeter of and a width of

Explanation

We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.

Subtract from both sides

Divide by both sides

$\frac{50}{2}=\frac{2l}{2}$

A square has perimeter 1.

True or false: The area of the square is $\frac{1}{2}$ .

False

True

Explanation

All four sides of a square have the same length, so the common sidelength is one fourth of the perimeter. The perimeter of the given square is 1, so the length of each side is $\frac{1}{4}$ .

The area of a square is equal to the square of the length of a side, so the area of this square is

$A =\left ( \frac{1}{4} \right )^{2} = \frac{1^{2} }{4^{2} } = \frac{1}{16}$ .

A square has diagonals of length 1. True or false: the area of the square is $\frac{1}{2}$ .

True

False

Explanation

Since a square is a rhombus, its area is equal to half the product of the lengths of its diagonals. Each diagonal has length 1, so the area is equal to

$A = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2}$ .