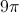How to find the volume of a cylinder
Help Questions
Math › How to find the volume of a cylinder
What is the volume of a cylinder with a radius of 6 meters and a height of 11 meters? Use 3.14 for 
Note: The formula for the volume of a cylinder is:
Explanation
To calculate the volume, you must plug into the formula given in the problem. When you plug in, it should look like this: 

What is the volume of a hollow cylinder with an outer diameter of 


Explanation
The general formula for the volume of a hollow cylinder is given by 



The question gives diameters and we need to convert them to radii by cutting the diameters in half. Remember, 

What is the surface area of a cylinder with a radius of 2 cm and a height of 10 cm?
40π cm2
32π cm2
56π cm2
48π cm2
36π cm2
Explanation
SAcylinder = 2πrh + 2πr2 = 2π(2)(10) + 2π(2)2 = 40π + 8π = 48π cm2
What is the surface area of a cylinder with a base diameter of 

None of the answers
Explanation
Area of a circle
Circumference of a circle
Surface area of a cylinder
The volume of a cylinder is 

Explanation
The volume of a cylinder is equal to:
Use this formula and the given radius to solve for the height.
Now that we know the height, we can solve for the surface area. The surface area of a cylinder is equal to the area of the two bases plus the area of the outer surface. The outer surface can be "unwrapped" to form a rectangle with a height equal to the cylinder height and a base equal to the circumference of the cylinder base. Add the areas of the two bases and this rectangle to find the total area.
Use the radius and height to solve.
What is the volume of a cylinder with a radius of 

Explanation
When thinking of a 3D figure, think of it as a stack of something. In this case, a cylinder is a stack of a circles.
The volume will be the area of that base circle times the height of the cylinder. Mathematically that would be 
Plug in our given values and solve.
Calculate the volume of a cylinder with a height of six, and a base with a radius of three.
Explanation
The volume of a cylinder is give by the equation 
In this example, 

This figure is a right cylinder with radius of 2 m and a height of 10 m.
What is the volume of the right cylinder (m3)?
Explanation
The formula for the volume of a right cylinder is 



A sphere with a radius of 
Not enough information to solve
Explanation
In order to solve this problem, one key fact needs to be understood. A sphere will take up exactly 
First, we need to find the volume of the sphere.
This equals 
What is the volume of a cylinder with a radius of 2 and a length that is three times as long as its diameter?
Explanation
The volume of a cylinder is the base multiplied by the height or length. The base is the area of a circle, which is