How to find the area of an equilateral triangle
Help Questions
Math › How to find the area of an equilateral triangle
Triangle A: A right triangle with sides length 

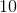
Triangle B: An equilateral triangle with side lengths 
Which triangle has a greater area?
Triangle B
Triangle A
The areas of the two triangles are the same.
There is not enough information given to determine which triangle has a greater area.
Explanation
The formula for the area of a right triangle is 


The formula for the area of an equilateral triangle is 

To determine which of the two areas is greater without using a calculator, rewrite the areas of the two triangles with comparable factors. Triangle A's area can be expressed as 



Find the area of an equilateral triangle whose perimeter is
Explanation
The formula for the perimeter of an equilateral triangle is:
Plugging in our values, we get
The formula for the area of an equilateral triangle is:
Plugging in our values, we get
What is the area of an equilateral triangle with side 11?
Explanation
Since the area of a triangle is
you need to find the height of the triangle first. Because of the 30-60-90 relationship, you can determine that the height is 
Then, multiply that by the base (11).
Finally, divide it by two to get 52.4.
What is the area of an equilateral triangle with sides 12 cm?
36√3
12√2
72√3
54√2
18√3
Explanation
An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side. So Atriangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm2.

What is the area of an equilateral triangle with a side length of 
Not enough information to solve
Explanation
In order to find the area of the triangle, we must first calculate the height of its altitude. An altitude slices an equilateral triangle into two 



Therefore, we can find the height of the altitude of this triangle by designating a value for 



Now, we can calculate the area of the triangle via the formula 
Find the area of the following equilateral triangle:
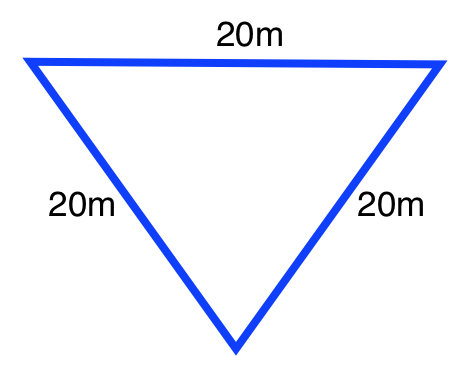
Explanation
The formula for the area of an equilateral triangle is:
Where 
Plugging in our values, we get:

An equilateral triangle has a side length of 
Not enough information to solve
Explanation
In order to find the area of the triangle, we must first calculate the height of its altitude. An altitude slices an equilateral triangle into two 



Therefore, we can find the height of the altitude of this triangle by designating a value for 

that 

Now, we can calculate the area of the triangle via the formula
Now convert to meters.
A circle contains 6 copies of a triangle; each joined to the others at the center of the circle, as well as joined to another triangle on the circle’s circumference.
The circumference of the circle is
What is the area of one of the triangles?
Explanation
The radius of the circle is 2, from the equation circumference 
To find the height of this triangle, we must divide it down the centerline, which will make two identical 30-60-90 triangles, each with a base of 1 and a hypotenuse of 2. Since these triangles are both right traingles (they have a 90 degree angle in them), we can use the Pythagorean Theorem to solve their height, which will be identical to the height of the equilateral triangle.
We know that the hypotenuse is 2 so 

Now our formula looks like this: 

Let's subtract 1 from each side of that equation, in order to make things a bit simpler:
Now let's apply the square root to each side of the equation, in order to change 

Therefore, the height of our equilateral triangle is
To find the area of our equilateral triangle, we simply have to multiply half the base by the height:
The area of our triangle is
Determine the area of the following equilateral triangle:

Explanation
The formula for the area of an equilateral triangle is:

where 
Plugging in our value, we get:
The area of square ABCD is 50% greater than the perimeter of the equilateral triangle EFG. If the area of square ABCD is equal to 45, then what is the area of EFG?
30
25√3
50
25
50√3
Explanation
If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.
The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.
We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√ 3.
In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s2/4.




































































